二进制转格雷码
反射二进制码或格雷码是对二进制数系统的一种排序,使得两个连续的值只在一位(二进制位)上有所不同。格雷码在硬件生成的二进制数的正常序列中非常有用,因为这些序列在从一个数字转换到下一个数字的过程中可能会导致错误或歧义。因此,格雷码可以轻松解决这个问题,因为在任意两个数字之间的转换过程中只有一位改变其值。
二进制转格雷码
格雷码用于旋转和光电编码器、卡诺图和错误检测。两个相邻格雷码的汉明距离始终为1,并且第一个格雷码和最后一个格雷码的汉明距离也始终为1,因此它也称为循环码。
使用卡诺图 (K) −您可以使用其他方法构造格雷码,但它们可能无法像上述方法那样并行执行。例如,可以使用如下所示的 K 图构造 3 位格雷码
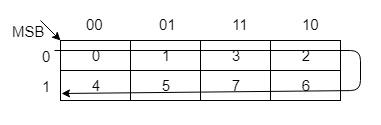
| 十进制 | 二进制 | 格雷码 |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
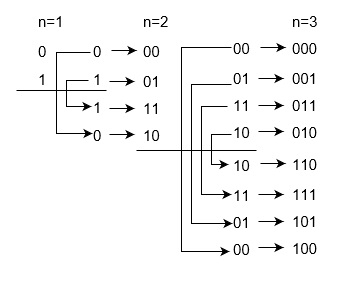
使用反射和前缀法 −
n位格雷码可以使用如下解释的反射和前缀法递归生成。
- 生成 n=1 的代码:0 和 1 代码。
- 按顺序取之前的代码:0 和 1。
- 在以下列表中添加反转的代码:0、1、1 和 0。
- 现在为原始的先前代码添加前缀 0,为新生成的代码添加前缀 1:00、01、11 和 10。
因此,格雷码 0 和 1 分别对应于二进制数 0 和 1。格雷码:00、01、11 和 10 分别对应于二进制数:00、01、10 和 11。类似地,您可以为 3 位二进制数构造格雷码
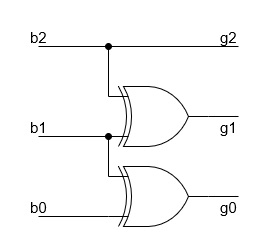
使用异或 (⊕) 运算 −
这是一种从二进制数获得格雷码的非常简单的方法。以下是针对 n 位二进制数的步骤 −
- 格雷码的最高有效位 (MSB) 始终等于给定二进制码的 MSB。
- 输出格雷码的其他位可以通过对索引处的二进制码位和前一个索引进行异或运算来获得。
例如,对于 3 位二进制数,设二进制数字为 b2、b1、b0,其中 b2 是最高有效位 (MSB),b0 是二进制的最低有效位 (LSB)。格雷码数字为 g2、g1、g0,其中 g2 是最高有效位 (MSB),g0 是格雷码的最低有效位 (LSB)。
| 二进制 b2 b1 b0 | 格雷码 g2 g1 g0 |
|---|---|
| 000 | 000 |
| 001 | 001 |
| 010 | 011 |
| 011 | 010 |
| 100 | 110 |
| 101 | 111 |
| 110 | 101 |
| 111 | 100 |
因此,使用 k 图求解布尔表达式,将得到 g2=b2,g1=b1⊕b2,以及 g0=b0⊕b1。
类似地,您可以将 n 位 (bnb(n-1)...b2b1b0) 二进制数转换为格雷码 (gng(n-1)...g2g1g0)。对于最低有效位 (LSB) g0=b0⊕b1,g1=b1⊕b2,g2=b1⊕b2,…… g(n-1)=b(n-1)⊕bn,gn=bn。
示例 − 将二进制数 111010 转换为格雷码。
因此,根据上述算法,
g0=b0⊕b1 = 0⊕1 = 1
g1=b1⊕b2 = 1⊕0 = 1
g2=b2⊕b3 = 0⊕1 = 1
g3=b3⊕b4 = 1⊕1 = 0
g4=b4⊕b5 = 1⊕1 = 0
g5=b5 = 1 = 1
因此,格雷码将是 100111。


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP