格雷码是什么？

反射二进制码或格雷码是对二进制数系统的一种排序，使得两个连续的值仅在一个比特（二进制数字）上不同。格雷码在硬件生成的二进制数的正常序列中非常有用，因为从一个数字到下一个数字的转换可能会导致错误或歧义。因此，格雷码可以轻松地消除此问题，因为在两个数字之间的任何转换期间，只有一个比特改变其值。

格雷码不是加权的，这意味着它不依赖于数字的位置值。这是一种循环变量码，这意味着从一个值到下一个值的每次转换都只涉及一个比特的变化。

格雷码也称为反射二进制码，因为前 (n/2) 个值与后 (n/2) 个值相同，但顺序相反。

构造一个 n 位格雷码

n 位格雷码可以使用反射和前缀方法递归生成，如下所述。

  • 生成 n=1 的代码：0 和 1 代码。
  • 按顺序取之前的代码：0 和 1。
  • 在以下列表中添加反转的代码：0、1、1 和 0。
  • 现在为原始的先前代码添加前缀 0，为新生成的代码添加前缀 1：00、01、11 和 10。

因此，格雷码 0 和 1 分别对应于二进制数 0 和 1。格雷码：00、01、11 和 10 分别对应于二进制数：00、01、10 和 11。类似地，您可以为 3 位二进制数构造格雷码

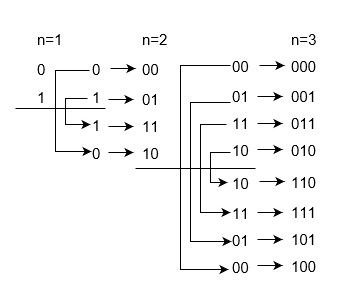
因此，格雷码如下所示：

对于 n = 1 位
对于 n = 2 位
对于 n = 3 位
二进制
格雷码
二进制
格雷码
二进制
格雷码
0
0
00
00
000
000
1
1
01
01
001
001
 
10
11
010
011
11
10
011
010
 
100
110
101
111
110
101
111
100

从 Gn 生成 G(n+1) 的迭代方法如下所示。这是一种更简单的构造 n 位二进制数的格雷码的方法。如果输入值的下一个较高位设置为 1，则每个位都被反转。第 n 个格雷码是通过计算 n⊕(floor(n/2)) 获得的。

  • Gn 是从 0 到 (2n-1) 的排列的唯一数字。
  • Gn 嵌入到 G(n+1) 的前半部分，后半部分为 G(n+1) 的反序。
  • 在前一半的每个数字中添加前缀 0，在后一半的每个数字中添加前缀 1。

两个相邻格雷码的汉明距离始终为 1，并且第一个格雷码和最后一个格雷码的汉明距离也始终为 1，因此它也称为 循环码。

您可以使用其他方法构造格雷码，但它们可能无法像上面给出的方法那样并行执行。例如，可以使用 K 映射构造 3 位格雷码，如下所示

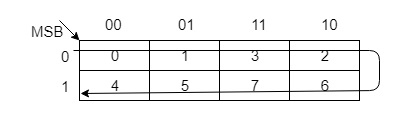
十进制
二进制
格雷码
0
000
000
1
001
001
2
010
011
3
011
010
4
100
110
5
101
111
6
110
101
7
111
100

格雷码的类型

还有其他类型的格雷码，例如贝克特-格雷码、单轨格雷码等。

  • N 进制格雷码，其中包含非布尔值，例如 1、2、3 的序列。
  • 二维 (n,k) 格雷码用于纠错。
  • 平衡格雷码具有相等的转换计数。

格雷码的用途

格雷码用于旋转和光学编码器、卡诺图和错误检测。

更新时间： 2023年11月1日

41K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告