如何在 Python 中使用 SciPy 计算矩阵的特征值和特征向量？

特征向量和特征值在许多情况下都有应用。德语中“Eigen”的意思是“自己的”或“典型的”。特征向量也被称为“特征向量”。假设我们需要对数据集执行一些转换，但给定的条件是数据集中的数据方向不应该改变。这时可以使用特征向量和特征值。

给定一个方阵（行数等于列数的矩阵），特征值和特征向量满足以下等式。

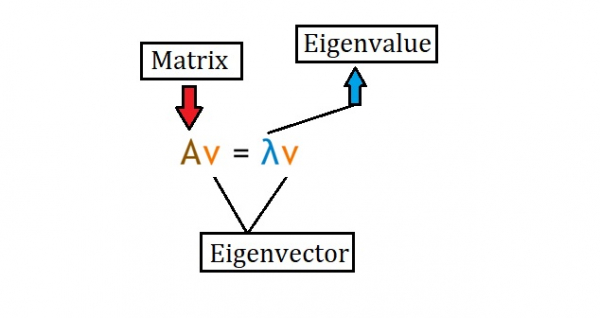
在找到特征值后计算特征向量。

注意 - 特征值也适用于 3 维或更高维。

SciPy 在库中提供了一个名为“eig”的函数，可以帮助计算特征值和特征向量，而不是手动执行这些数学计算。

“eig”函数的语法

scipy.linalg.eig(matrix)

让我们看看如何使用“eig”函数 -

示例

 现场演示

from scipy import linalg
import numpy as np
my_arr = np.array([[5,7],[11,3]])
eg_val, eg_vect = linalg.eig(my_arr)
print("The Eigenvalues are :")
print(eg_val)
print("The Eigenvectors are :")
print(eg_vect)

输出

The Eigenvalues are :
[12.83176087+0.j -4.83176087+0.j]
The Eigenvectors are :
[[ 0.66640536 -0.57999285]
[ 0.74558963 0.81462157]]

解释

  • 导入所需的库。
  • 使用 Numpy 库在矩阵中定义一些值。
  • 将矩阵作为参数传递给“eig”函数，该函数计算矩阵的特征值和特征向量。
  • 这些计算出的数据存储在两个不同的变量中。
  • 此输出显示在控制台上。

更新于: 2020-12-10

1K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始
广告