数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究如何在 SciPy Python 中执行离散傅里叶变换？
离散傅里叶变换（DFT）是一种数学技术，有助于将空间数据转换为频率数据。
快速傅里叶变换（FFT）是一种旨在计算空间数据的离散傅里叶变换的算法。
空间数据通常以多维数组的形式存在。频率数据是指包含特定时间段内信号或波长数量的信息的数据。
让我们看看如何使用“SciPy”库来实现此 DFT。
该图是使用 matplotlib 库创建的，数据是使用 Numpy 库生成的。
示例
From matplotlib import pyplot as plt
import numpy as np
my_freq = 6
freq_samp = 70
time_val = np.linspace(0, 3, 3 * freq_samp, endpoint = False )
amp_val = np.sin(my_freq * 3 * np.pi * time_val)
figure, axis = plt.subplots()
axis.plot(time_val, amp_val)
axis.set_xlabel ('Time (in seconds)')
axis.set_ylabel ('Amplitude of signal')
plt.show()
from scipy import fftpack
A = fftpack.fft(amp_val)
frequency = fftpack.fftfreq(len(amp_val)) * freq_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-freq_samp / 2, freq_samp/ 2)
axis.set_ylim(-7, 125)
plt.show()输出
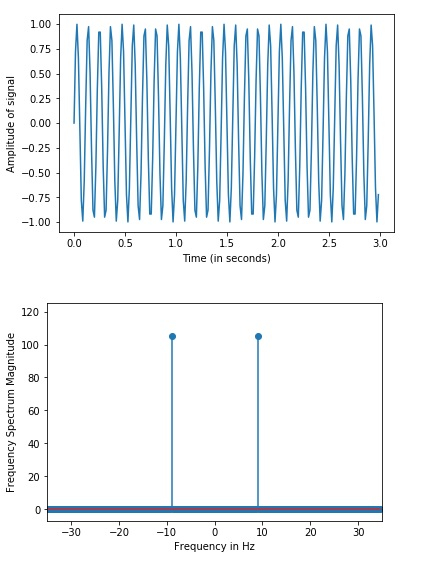
解释
- 导入所需的包。
- 借助 Numpy 库生成数据。
- 借助 matplotlib 库，此数据在控制台上绘制为正弦波。
- 接下来，使用“fftpack”包查找生成数据的快速傅里叶变换。
- 此数据再次绘制在图表上。
更新于： 2020-12-10
402 次查看
广告