分贝运算如何通过对数进行？

---

dB运算简介

“分贝”是使用对数刻度而不是线性刻度表示比率的一种方式。它们被应用于**STEM**的多个学科。在本文中，我们将通过与电气工程相关的示例来了解如何进行使用分贝的计算。我们知道，“分贝”表示两个量在对数刻度上的比率。比较两个量时，其中一个将被视为参考量。本文讨论了可以对分贝进行的一些基本运算以及一些示例。

基于对数的基本运算

对数乘法

在线性刻度上取的两个数的乘积的对数等于这两个数在其对数形式下的和。

我们知道，线性刻度上的乘法等效于对数刻度上的加法。

(A×B)_dB=(A)_dB + (B)_dB

其中，

A(dB)=10log₁₀A

让我们考虑一个级联的三级放大器系统，其中第一、第二和第三个放大器的增益分别为10、15和20。馈送到第一个放大器的信号的输入功率为5瓦。

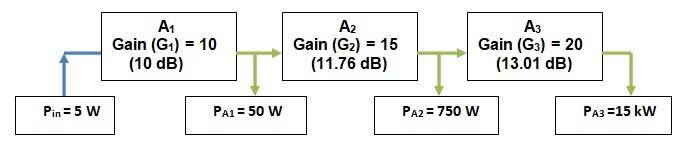
系统的总增益是P_A3 / P_in的比率。

系统的总线性增益是各个放大器线性增益的乘积。这使得我们的总线性增益A_P为

$$A_{p}=\frac{P_{A3}}{P_{in}}=G_{1}G_{2}G_{3}=3000$$

$$P_{A3}=A_{P}P_{in}=15kW$$

总“dB”功率增益为

10 log₁₀3000=34.77dB

我们也知道，系统的总增益是放大器各个“dB”增益的总和。由于我们处理的是功率比，

$$10log_{10}(A\times\:B\times\:C)=10log_{10}A +10log_{10}B+10log_{10}C$$

$$10log_{10}(10\times\:15\times\:20)=10log_{10}10 +10log_{10}15+10log_{10}20$$

$$=10dB+11.76dB+13.01dB$$

对数除法

在线性刻度上取的两个数的除法的对数等于这两个数在其对数形式下的差。

$$(A/B)_{dB}=A_{dB}-(B)_{dB}$$

其中

$$A(dB)=10log_{10}A$$

因此，我们有

$$log_{10}10-log_{10}5=log_{10}(\frac{10}{5})=log_{10}2$$