数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究独立顶点集
独立集用集合表示，其中
不应该有**任何彼此相邻的边**。任何两条边之间都不应该有公共顶点。
不应该有**任何彼此相邻的顶点**。任何两个顶点之间都不应该有公共边。
独立顶点集
设'G' = (V, E) 为一个图。如果'S' 中的任何两个顶点都不相邻，则'V' 的子集称为'G' 的独立集。
示例
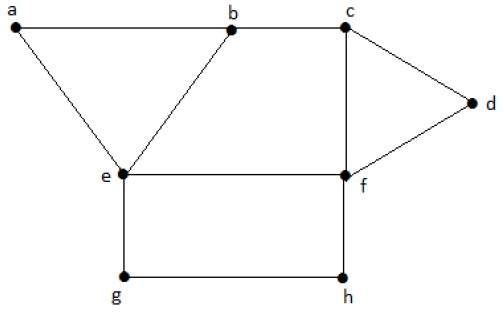
考虑上述图形中的以下子集：
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}显然，S1 不是一个独立顶点集，因为要获得一个独立顶点集，必须至少有两个顶点以图的形式存在。但这里情况并非如此。子集 S2、S3 和 S4 是独立顶点集，因为没有顶点与子集中的任何顶点相邻。
最大独立顶点集
设'G' 为一个图，则如果不能将'G' 的任何其他顶点添加到'S'，则'G' 的独立顶点集称为最大独立顶点集。
示例
考虑上述图形中的以下子集。
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}S2 和 S3 是'G' 的最大独立顶点集。在 S1 和 S4 中，我们可以添加其他顶点；但在 S2 和 S3 中，我们不能添加任何其他顶点。
最大独立顶点集
具有最大顶点数的'G' 的最大独立顶点集称为最大独立顶点集。
示例
考虑上述图形中的以下子集：
S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}只有 S3 是最大独立顶点集，因为它包含最多的顶点。'G' 的最大独立顶点集中的顶点数称为'G' 的独立顶点数 (β2)。
示例
For the complete graph Kn, Vertex covering number = α2 = n-1 Vertex independent number = β2 = 1 You have α2 + β2 = n In a complete graph, each vertex is adjacent to its remaining (n − 1) vertices. Therefore, a maximum independent set of Kn contains only one vertex. Therefore, β2=1 and α2=|v| − β2 = n-1
注意 - 对于任何图'G' = (V, E)
α2 + β2 = |v|
如果'S' 是'G' 的独立顶点集，则 (V – S) 是'G' 的顶点覆盖。
更新于：2019年8月23日
305 次浏览
广告