数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用 Python 查找无向图中是否存在给定大小的独立集
假设我们有一个给定的无向图；我们需要检查它是否包含大小为 l 的独立集。如果存在大小为 l 的独立集，则返回“Yes”，否则返回“No”。
我们需要记住，图中的独立集定义为一组顶点，这些顶点彼此之间没有直接连接。
所以，如果输入类似于 L = 4，
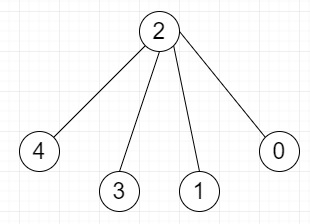
那么输出将是 yes
为了解决这个问题，我们将遵循以下步骤：
定义一个函数 is_valid()。它将接收图和数组 arr 作为参数。
从 i = 0 到 arr 的大小循环：
从 j = i + 1 到 arr 的大小循环：
如果 graph[arr[i], arr[j]] 等于 1，则：
返回 False
返回 True
定义一个函数 solve()。它将接收图、数组 arr、k、索引 index 和数组 sol 作为参数。
如果 k 等于 0，则：
如果 is_valid(graph, arr) 等于 True，则：
sol[0] := True
返回
否则，
如果 index >= k，则：
返回 (solve(graph, arr[从索引 0 到结束] 连接一个包含 [index] 的列表, k-1, index-1, sol) 或 solve(graph, arr[从索引 0 到结束], k, index-1, sol))
否则，
返回 solve(graph, arr[从索引 0 到结束] 连接一个包含 [index] 的列表, k-1, index-1, sol)
示例
让我们看看以下实现，以更好地理解：
def is_valid(graph, arr):
for i in range(len(arr)):
for j in range(i + 1, len(arr)):
if graph[arr[i]][arr[j]] == 1:
return False
return True
def solve(graph, arr, k, index, sol):
if k == 0:
if is_valid(graph, arr) == True:
sol[0] = True
return
else:
if index >= k:
return (solve(graph, arr[:] + [index], k-1, index-1, sol) or solve(graph, arr[:], k, index-1, sol))
else:
return solve(graph, arr[:] + [index], k-1, index-1, sol)
graph = [
[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1]]
k = 4
arr = []
sol = [False]
solve(graph, arr[:], k, len(graph)-1, sol)
if sol[0]:
print("Yes")
else:
print("No")输入
[[1, 1, 0, 0, 0], [1, 1, 1, 1, 1], [0, 1, 1, 0, 0], [0, 1, 0, 1, 0], [0, 1, 0, 0, 1]], 4
输出
Yes
更新于: 2020年8月25日
238 次浏览
广告