截距

---

介绍

• 坐标图也称为坐标网格或平面。

• 在坐标网格中，两条垂直线称为轴。

• 水平轴称为x轴，垂直轴称为y轴。

• 在网格中，点分布在数轴上，即x轴和y轴上。

• 接触点以有序对的形式写出。通过读取坐标平面的经纬度，可以找到网格上点的坐标。

• x轴上的点称为x坐标，y轴上的点称为y坐标。

截距

• 截距基本上是图中交点的坐标。

• 如果一条直线在一点与x轴相交，则该点称为x截距；y截距是直线与y轴相交的点。

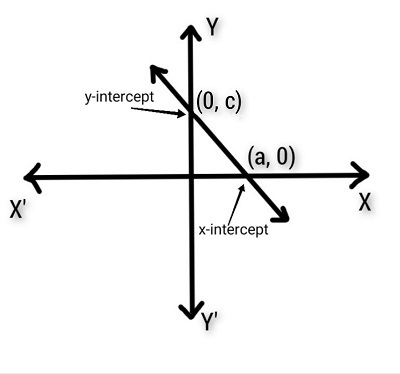
直线在坐标轴上的截距

当一条直线在B点与x轴相交，在C点与y轴相交时，OB和OC分别称为该直线在x轴和y轴上的截距。

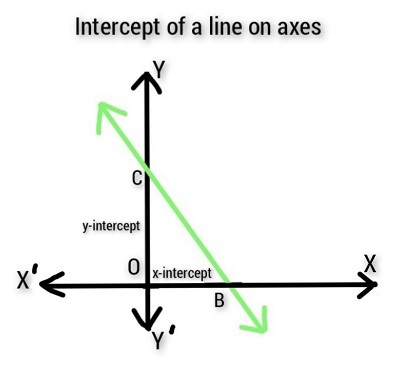
直线在圆锥曲线上的截距

一条直线在固定点与一条垂直线相交，围绕该点旋转形成一个称为双圆锥的曲面。当双圆锥与平面相交时，会形成二维曲线。这些曲线称为圆锥曲线。

平面与双圆锥相交形成四种圆锥曲线。

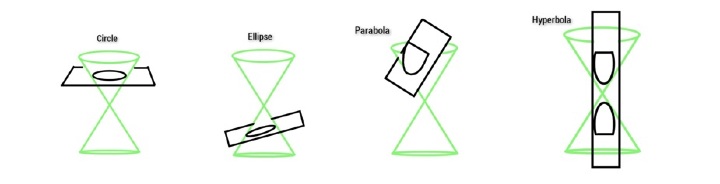
当直线与圆锥曲线相交时，就会有解。截距将表示为有序对。

在图中，如果一条直线与圆锥曲线不相交，则无解。这意味着在平面上找不到截距。

例如：

一条直线Ax + By = C与双曲线 (x-h)²/a² - (y-k)²/b² = 1 相交

则直线将在点P(x₁,y₁)和Q(x₂,y₂)与双曲线相交，其中P和Q称为交点。

直线方程：斜率-截距式

当一条直线与坐标轴相交时，它在坐标图中与一个或两个点相交。

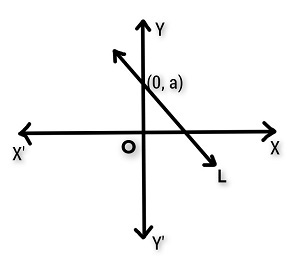
在上图中，给定直线的y截距是距离a。

从图的原点到直线与y轴交点的单位距离是a。

点斜式直线方程为 y - y₁ = m(x - x₁)

斜率为m且经过点(0, a)的直线方程为：

y - a = m(x - 0 其中 (0,a) 为 (x₁,y₁))

y = mx + a

因此，y = mx + a是直线的斜率-截距式方程。

直线方程：截距式

当一条直线与坐标轴相交时，它在坐标图的x轴和y轴上分别与一个点相交。

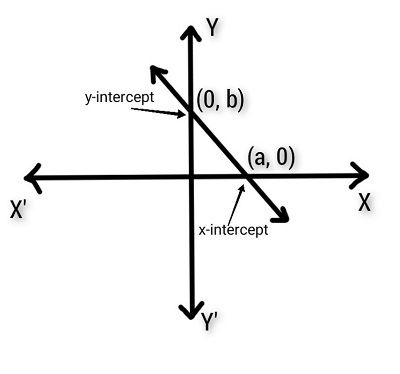
在上图中，直线与两点 (a,0) 和 (0,b) 相交。

两点式直线方程为 (y - y₁) = (y₂ - y₁)/(x₂ - x₁)(x - x₁)

因此，与两点 (a,0) (x₁,y₁) 和 (0,b) = (x₂,y₂) 相交的直线方程为：

(y - 0) = (b - 0)/(0 - a)(x - a)

-ay = bx - ab

=> bx + ay = ab .........(1)

将(1)式两边除以ab，得到：

bx/ab + ay/ab = ab/ab

通过约去公因式，我们得到截距式直线方程：

x/a + y/b = 1

例题

1. 从下图中，找出直线的截距。

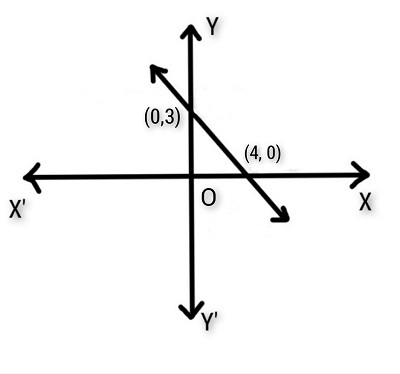
解：

直线与x轴相交于 (4,0)，与y轴相交于 (0,3)。

因此，直线在坐标轴上的截距为 (4,0) 和 (0,3)。

2. 在给定的直线 7x + 9y = 14 中，求x截距和y截距。

解：

直线方程为 7x + 9y = 14

要找到该直线的x截距，令 y = 0

7x + 9(0) = 14

=> 7x = 14

x = 2

要找到该直线的y截距，令 x = 0

7(0) + 9y = 14

=> 9y = 14

y = 14/9

因此，x截距 = 2，y截距 = 14/9

如果经过 (1,2) 的直线的斜率为 -5/7

3. 求直线方程

解：

直线的斜率-截距式方程为 y = mx + a

将 m = -5/7 代入 y = mx + a，得到

2 = -5/7(1) + a

14 = -5 + a

=> a = 19

因此，直线方程为 7y = -5x + 19

4.如果直线方程为 6x + 3y = 12。将直线方程表示为截距式，并求x截距和y截距。

解：

直线方程为 6x + 3y = 12.......(1)

将(1)式两边除以12，得到：

6x/12 + 3y/12 = 12/12

x/2 + y/4 = 1 是直线的截距式方程

因此，x截距 = 2，y截距 = 4

结论

• 在坐标图中，水平轴称为x轴，垂直轴称为y轴。

• 当一条直线在一点与x轴相交时，该点称为x截距；y截距是直线与y轴相交的点。

• x轴上的点称为x坐标，y轴上的点称为y坐标。

• 直线方程为 x/a + y/b = 1，其中a和b分别是直线的x截距和y截距。

• 直线的斜率-截距式方程为 y = mx + a

常见问题

1. 谁引入了坐标系？

• 坐标系，也称为笛卡尔平面，是以法国数学家勒内·笛卡尔的名字命名的。

• 他是第一个在坐标平面上引入几何问题求解方法的人。

• 他被称为解析几何之父。

2. 谁发明了圆锥曲线？

希腊数学家梅内克穆斯介绍了圆锥曲线的概念。

3. 圆的一般方程是什么？它是如何从双圆锥形成的？

圆的一般方程为 (x - h)² + (y - k)² = a²

其中a是半径，(h, k)是圆心。

• 圆锥曲线的底部曲面是一个圆。

• 当平面与双圆锥水平相交时，会形成一个圆。

• 当平面垂直于轴时，椭圆会变成圆。

4. 什么是退化圆锥曲线？

如果平面与双圆锥的顶点相交，则形成的图形称为退化圆锥曲线。

5. 给出解析几何的一些实际应用。

• 为了确保飞行安全，解析几何用于更新航班的位置。

• 它用于收集卫星位置信息。

• 地球的经纬度可以用坐标系来描述。

• 可以用解析几何来预测风暴未来的路径。

• 地图上城市和州的位置是借助解析几何来定位的。