温度的动理论解释

---

简介

物质有五种状态，气体是其中之一。空隙被气体填充。大气充满了气体分子。它包含不同的气体分子。氧气分子是呼吸所必需的，也存在于我们的大气中，以及许多其他气体分子。宇宙中的一切物质都由称为分子的微小粒子组成。它们彼此之间存在一定的吸引力。分子之间存在分子间引力。

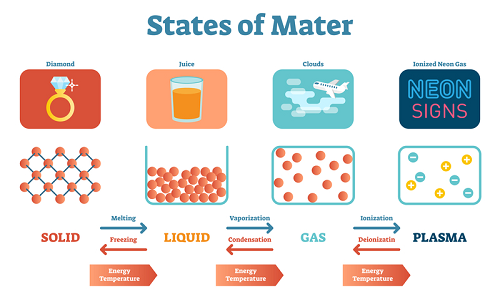
根据分子之间的吸引力，物质被分为五类。它们分别是固体、液体、气体、等离子体和玻色-爱因斯坦凝聚态。固体是分子间距离非常小且紧密结合在一起的物质。液体是分子间距离较小且结合不如固体紧密的物质。等离子体状态的分子具有较高的动能。

气体动理论的假设

气体动理论描述了气体的热力学行为。它们有一些基本的假设，如：

• 气体中存在许多称为粒子的微小粒子。

• 它们彼此之间以及与容器壁发生弹性碰撞。

• 这些粒子彼此相同，并且可以向所有可能的方向运动。

• 碰撞时间与碰撞之间的时间相比非常小。

• 与气体的总体积相比，分子的体积非常小。

• 除了碰撞时，分子之间不施加任何力。

• 分子之间的距离大于分子的尺寸。

• 所有分子都遵循运动定律。

温度的动理论解释是什么意思？

让我们考虑一个容积为V的充满气体的容器。假设分子以所有可能的速度运动。那么气体分子对器壁施加的压力由下式给出：

$\mathrm{P=\frac{1}{3}\frac{mnc^2}{v}}$

其中m表示一个分子的质量。n表示分子的数量。$\mathrm{C^2}$表示分子的均方根速度。V表示气体的体积。

1摩尔气体包含N个分子。

$\mathrm{PV=\frac{1}{3}mNC^2}$

根据气体定律PV=RT

$\mathrm{RT=\frac{1}{3}mNC^2}$

$\mathrm{\frac{RT}{N}=\frac{1}{3}mC^2}$

在等式右侧乘以2并除以2，我们得到：

$\mathrm{\frac{RT}{N}=\frac{2}{3} \times \frac{1}{2} mC^2}$

分子的动能为$\mathrm{K.E=\frac{1}{2}mC^2}$

$\mathrm{\frac{RT}{N}=\frac{2}{3} \times K.E}$

$\mathrm{K.E=\frac{3}{2}\times \frac{RT}{N}}$

$\mathrm{K.E=\frac{3}{2} KT}$

其中$\mathrm{K=\frac{R}{N}}$表示玻尔兹曼常数。

动能与温度之间的关系

作用于物体的功就是其能量。由于运动而具有能量的物体称为其动能。它可以从一个物体转移到另一个物体，也可以转化为其他形式的能量。这种能量取决于其质量和速度。动能的SI单位是焦耳。因此，物体的动能由下式给出：

$\mathrm{K.E=\frac{1}{2} mc^2}$

根据能量均分定理，分子的自由度不同；系统的总能量被平均分配到分子的每个自由度上。平均分配的能量为1/2 kT。这称为能量均分定理。因此，气体的温度与分子的动能直接相关。

气体定律

为了了解气体的行为，提出了许多定律。气体定律给出了压力、温度和体积之间的关系。它们是查理定律、盖-吕萨克定律、阿伏伽德罗定律、波义耳定律和格雷厄姆定律。

• 波义耳定律：波义耳定律明确指出，气体的压力与其体积成反比。（即）当压力增加时，体积会减小。只要温度保持恒定，就会保持这种关系。数学表示如下：

$\mathrm{P \varpropto \frac{1}{v}}$

$\mathrm{PV = k\:(常数)}$

• 查理定律：当温度升高时，气体膨胀。查理定律解释了这一点。它表明，当压力保持恒定时，气体的体积随温度的变化而直接变化。

$\mathrm{V \varpropto T}$

$\mathrm{\frac{v}{T} = k(常数)}$

• 盖-吕萨克定律：当气体的体积保持恒定时，气体的压力随温度的变化而直接变化。这称为盖-吕萨克定律。

$\mathrm{P \varpropto T}$

$\mathrm{\frac{P}{T} = k(常数)}$

• 阿伏伽德罗定律：阿伏伽德罗定律指出，在相同温度和压力下，相同体积的气体中，分子数量相同。

$\mathrm{V \varpropto n}$

$\mathrm{\frac{v}{n} = k}$

• 格雷厄姆定律：根据他的原理，较轻的分子比较重的分子运动得更快。即，在恒定压力和温度下，低分子质量分子的扩散速度快于高分子质量分子的扩散速度。扩散时间内的分子与它们质量密度的平方根成反比。

$\mathrm{r \varpropto \frac{1}{\sqrt{P}}}$

结论

在本教程中，详细讨论了气体动理论的假设和温度的动理论解释。还讨论了动能与温度以及气体定律之间的关系。

常见问题

Q1. 解释自由度。

A1. 描述分子位置所需的坐标数称为自由度。通常，单原子分子具有三个自由度。具有多个原子的分子包括三个额外的自由度，如平动、转动和振动。根据此，具有多个原子的分子的自由度会有所不同。

Q2. 说明气体中的平均自由程。

A2. 在气体中，分子彼此之间以及与容器壁发生碰撞。分子在任意两次连续碰撞之间行进的距离的平均值称为平均自由程。用λ表示。

Q3. 影响气体行为的因素有哪些？

A3. 影响气体行为的因素有温度（T）、压力（P）、体积和数量。如果气体的温度升高，气体膨胀，从而体积增加。类似地，由于气体分子压缩，温度降低时体积也降低。温度升高会导致气体膨胀，因此其压力也会升高，反之亦然。要将气体转化为固体或液体，温度必须非常低。数量和压力彼此成正比。由于压力与体积和数量成正比，因此可以通过提高数量和体积来增加压力。

Q4. 列出气体定律的一些应用？

A4. 如果环境条件发生变化，则气体分子的行为会偏离其正常行为。气体定律可以很好地研究这些变化。用于吸入液体的注射器遵循波义耳定律的原理。蛋糕和面包在加热时膨胀遵循查理定律。它也用于天气预报系统。它们还用于热力学和流体动力学。

Q5. 气体是如何被压缩的？

A5. 气体是物质的一种状态，其中分子松散地结合在一起。因此，分子之间存在许多空隙。当对气体施加压力时，这些空隙会减小，粒子会靠得更近。从而体积减小，气体被压缩。