气体动理论假设

---

介绍

在日常生活中，我们经常观察到光线透过小孔进入黑暗时空气分子的运动。气体动理论研究了空气分子的运动。借助动理论，可以根据气体存在的容器的压力(P)、体积(V)和温度(T)来定义气体的各种性质。微小粒子不会向上或向下移动，但它们可以向所有可能的方向移动。我们看不到这些粒子，因为它们的大小非常小，但我们能看到大粒子的运动。

Olivier Cleynen 和 User:Sharayanan，气体动理论 (2)，CC BY-SA 3.0

什么是气体动理论？

气体包含大量大小可忽略不计的粒子，称为分子。这些分子处于持续或不断的运动状态，或处于随机运动状态。在这次随机运动中，分子不断地以一定的速度运动，并与容器或其所存放容器的壁发生碰撞。

这些碰撞是完全弹性的，几乎是瞬时的（持续时间很短），分子在碰撞之间以直线运动并获得均匀的速度。

假设

• 粒子总是持续地向所有方向随机移动，但其运动轨迹是直线。

• 粒子不受任何吸引力或排斥力的影响。

• 气体是由大量具有小质量的微小粒子（如原子或分子）组成的集合。

• 粒子之间的空间非常大，因为粒子彼此相距很远。因此，与容器的体积相比，粒子的体积可以忽略不计。

• 粒子总是处于不断的运动状态，因此它们具有动能，动能与温度成正比。

• 由于微小粒子之间或与容器的碰撞，碰撞是完全弹性的，不会改变粒子的动量或能量。当粒子与容器碰撞时，也会对容器施加压力。这个压力取决于单位面积上碰撞的粒子数量。

动能和压力

我们知道动量是质量和速度的乘积。

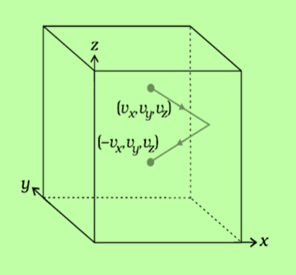
图2：分子在不同分量上的运动

分子动量的变化

$\mathrm{\Delta P=P_2-P_1}$

$\mathrm{\Delta P=mv_x-(-mv_x)}$

$\mathrm{P=2mv_x}$

连续碰撞的时间 $\mathrm{t=\frac{2A}{V_x}}$ 所以作用在壁上的力为

$\mathrm{F=\frac{\Delta P}{\Delta t}}$

$\mathrm{F=\frac{2mv_x}{2Av_x}}$

$\mathrm{F=m v_x^{2}}$

x方向上的压力，$\mathrm{P_x=\frac{F_x}{A}=\frac{m}{A^3}(v_x^{2})}$

同样，对于y方向 $\mathrm{P_y=\frac{m}{A^3}(v_y^{2})}$

以及对于z方向，$\mathrm{P_z=\frac{m}{A^3}(v_z^{2})}$

根据帕斯卡定律：

$\mathrm{P_x=P_y=P_z=P}$

我们可以写成，$\mathrm{P=\frac{P_x+P_y+P_z}{3}}$

现在代入所有方向的压力：

$\mathrm{P=\frac{m}{3A^3}(v_x^{2})+\frac{m}{3A^3}(v_y^{2})+\frac{m}{3A^3}(v_x^{2})}$

$\mathrm{P=\frac{m}{3A^3}(v_x^{2}+v_y^{2}+{v_z}^2)}$

$\mathrm{P=\frac{m}{3A^3}(v_{RMS}^2)}$

此外，我们可以写成，$\mathrm{P=\frac{1}{3}\rho (v_{RMS}^2).......(1)}$

其中 $\mathrm{v_{RMS}}$ - 均方根速度

$\mathrm{\rho}$ - 分子的密度

单位体积的动能：

$\mathrm{E=\frac{1}{2}\rho v^2...…(2)}$

将方程式 (1) 和 (2) 相除

$\mathrm{\frac{P}{E}=\frac{\frac{1}{3}\rho (v_{RMS}^2)}{\frac{1}{2} \rho v^2}=\frac{2}{3}}$

$\mathrm{P=\frac{2}{3}E}$

所以压力 $\mathrm{=\frac{2}{3}}$ 单位体积的动能

动能和温度

根据动理论

$\mathrm{P=\frac{1}{3}\rho (v_{RMS}^2)}$

$\mathrm{\rho=\frac{M}{v}}$

$\mathrm{P=\frac{1M}{3v}(v_{RMS}^2)}$

乘以并除以2

$\mathrm{PV=\frac{2}{3}\frac{1}{2}m(v_{RMS}^2)}$

$\mathrm{PV=\frac{2}{3}E}$

（我们知道 1 摩尔的理想气体方程 PV=RT）

$\mathrm{RT=\frac{2}{3}E}$

$\mathrm{E=\frac{3}{2}RT}$

每个分子的平均动能

$\mathrm{\overline{E}=\frac{E}{N}=\frac{3}{2}\frac{R}{N}T=\frac{3}{2}K_B T}$

N - 阿伏伽德罗常数

弛豫时间

这也被称为平均自由时间。粒子的运动是完全随机的。在它们的运动过程中，它们会发生碰撞并改变方向。每次碰撞都会使它们随机改变方向。

因此，在两次连续碰撞之间，两个粒子之间的平均时间或时间间隔称为弛豫时间。

平均自由程

在两次连续碰撞之间，分子以恒定速度沿直线路径运动。粒子相遇另一个粒子所走过的平均距离。并非每个路径长度或自由程都是相同的。它可能因不同的粒子而异。它用“λ”表示。

平均自由程：

$\mathrm{\lambda=\frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}(其中\:n=\frac{N}{V})}$

$\mathrm{\lambda=\frac{1}{\sqrt{2}\pi d^2 n}}$

其中 n 是单位体积内的分子数

d 是分子的直径

布朗运动

图片即将推出

图3：布朗运动

如果细小的粒子（原子或分子）悬浮（散布）在任何流体（液体或气体）中，它们就会开始向所有可能的方向进行随机运动，并彼此碰撞，并与它们所保持的容器碰撞，形成锯齿状路径。这种运动称为布朗运动。

植物学家罗伯特·布朗于 1827 年首次描述了这种运动，因此为了纪念他，这种运动被称为布朗运动，当时他用显微镜观察浸在液体中的花粉粒。

后来在 1905 年，爱因斯坦提出了他的布朗运动理论。花粉粒由于粒子的碰撞或轰击而随机移动。这就是爱因斯坦在他的论文中所展示的。让·佩兰证实了这一解释，并因此获得了 1926 年的诺贝尔奖。在阳光照射到布满灰尘的房间时，可以观察到一些现象。我们观察到灰尘粒子随机移动。

结论

气体动理论有助于理解粒子的宏观性质或微观性质。通过知道温度，我们可以很容易地找到平均动能，因为动能与温度成正比。所有这些都可以在原子理论中进行研究。气体动理论的结论是粒子总是在运动。

常见问题

Q1。均方根分子速度取决于哪些量？

答：我们知道，$\mathrm{v_{RMS}=\sqrt{\frac{3RT}{M}}}$

气体的速度是

• 与绝对温度成正比

• 与气体的摩尔质量成反比

此外，$\mathrm{摩尔质量=\frac{体积}{摩尔}}$

$\mathrm{摩尔质量=\frac{体积}{\frac{质量}{M}}}$

因此，摩尔体积与气体的均方根速度成正比。

Q2。一辆装有货物的卡车以均匀速度行驶。放在卡车上的罐装气体内部的气体分子温度是多少？

答：分子获得相对速度，均方根速度与横向平移不同。

Q3。气体分子平均动能取决于哪些因素？

答：气体原子或分子的平均动能取决于温度，因为动能与绝对温度成正比。

$\mathrm{K=\frac{3}{2}\frac{R}{N_A}T}$

Q4。如果氢气和氧气样品的体积相同，那么哪个样品的分子数量更多？

答：如果两个样品的体积相同，则气体的温度和压力相同。结果，两个样品的分子数量相同。

Q5。氢 (H) 分子的温度和均方根速度在 79°C 时等于氧 (O) 分子的温度和均方根速度。

答：我们知道：

$\mathrm{v_{RMS}=\sqrt{\frac{RT}{M}}}$

氧分子的均方根速度等于氢的均方根速度。

$\mathrm{\sqrt{\frac{273+79}{32}}=\sqrt{\frac{T}{2}}}$

$\mathrm{\frac{352}{32}=\frac{T}{2}}$

$\mathrm{11\:\times\:2=T}$

$\mathrm{T=22^{\circ}C}$

因此需要 22°C 的温度。