
Matlab矩阵 - 快速指南
Matlab矩阵 - 简介
MATLAB(矩阵实验室)是一种第四代高级编程语言和交互式环境,用于数值计算、可视化和编程。它允许进行矩阵操作;函数和数据的绘图;算法的实现;用户界面的创建;与用其他语言编写的程序(包括 C、C++、Java 和 FORTRAN)的接口;分析数据;开发算法;以及创建模型和应用程序。
在本教程中,我们将重点介绍使用 MATLAB 实现矩阵。
矩阵
矩阵是由按行和列排列的数字组成的集合,表示一个矩形数组。
下面显示了一个具有 2 行 3 列的矩阵示例
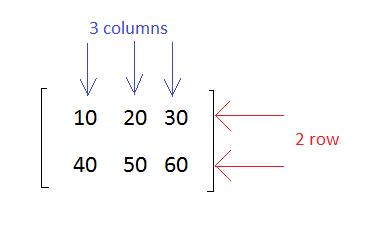
矩阵维度
矩阵的维度根据行数和列数定义。
具有 2 行 3 列的矩阵称为 2x3 矩阵。
具有 3 行 3 列的矩阵称为 3x3 矩阵。
Matlab中的矩阵
在 MATLAB 中,您可以通过输入每一行中以逗号或空格分隔的数字,并使用分号标记每一行的结束来创建矩阵。
示例
要创建一个 4x5 矩阵,请输入以下内容。
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
该矩阵有 4 行 5 列。
第一行将具有 1 2 3 4 5 这些值
第二行:2 3 4 5 6
第三行:3 4 5 6 7
第四行:4 5 6 7 8
输出
大小为 4x5 的矩阵如下所示
a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8
让我们在 MATLAB 命令窗口中测试矩阵创建,如下所示 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >>
引用元素
要引用矩阵 mx 中第 m 行第 n 列的元素,我们编写以下内容
mx(m, n);
示例
要引用在上节中创建的矩阵 a 中第 2 行第 5 列的元素,我们输入以下内容。
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(2,5) ans = 6 >>
要获取矩阵中第 n 列的所有元素,您可以使用 A(:,n),其中 n 表示矩阵中的列号。
A(:,n).
示例
现在,让我们从矩阵 a 的第 4 列的所有元素创建一个列向量 v。这将如下所示
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; v = a(:,4)
输出
MATLAB 将执行上述语句并返回以下结果。
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> v=a(:,4) v = 4 5 6 7 >>
您还可以选择第 m 到第 n 列中的元素。为此,我们编写如下内容。
a(:,m:n)
示例
让我们通过获取第二列和第三列的元素创建一个较小的矩阵,如下所示 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
输出
MATLAB 将执行上述语句并返回以下结果 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(:, 2:3) ans = 2 3 3 4 4 5 5 6 >>
同样,您可以通过获取矩阵的一部分来创建子矩阵。
示例
让我们通过获取 a 的内部子部分创建一个子矩阵 sab,如下所示 -
3 4 5 4 5 6
在 MATLAB 命令窗口中执行期间,矩阵将如下所示 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> sa = a(2:3,2:4) sa = 3 4 5 4 5 6 >>
Matlab矩阵 - 环境设置
MATLAB 的官方网站是 https://www.mathworks.com。
您的屏幕上将出现以下页面 -
要下载 MATLAB,请访问 https://in.mathworks.com/downloads/,如下所示 -
MATLAB 不是免费下载的,您需要支付许可证副本的费用。稍后您可以下载它。
提供了一个免费试用版本,您需要为您的帐户创建登录信息。创建帐户后,他们允许您下载 MATLAB 以及一个在线版本,试用期为 30 天的许可证。

完成从其网站创建登录信息后,下载 MATLAB 并安装到您的系统上。然后,启动 MATLAB,或者您也可以使用他们在您登录后可用的在线版本。
当您安装 matlab 或点击 MATLAB 的在线链接时,MATLAB 的 UI 界面如下所示。
了解 MATLAB 环境
MATLAB 开发 IDE 可以从桌面上创建的图标启动。MATLAB 中的主要工作窗口称为桌面。启动 MATLAB 时,桌面将以其默认布局显示。
正如我之前所说,如果您使用的是试用版,可以使用 MATLAB 的在线链接获取 IDE,如下所示 -
让我们了解 MATLAB IDE。
当前文件夹
此面板允许您访问项目文件夹和文件。
命令窗口
这是可以在命令行输入命令的主要区域。它由命令提示符 (>>) 表示。

工作区
工作区显示从文件创建和/或导入的所有变量。
Matlab矩阵 - 创建矩阵
在 MATLAB 中,您可以通过输入每一行中以逗号分隔的元素来创建矩阵。您还可以使用空格分隔的数字和分号来标记每一行的结束来创建矩阵。
单行矩阵
让我们在 MATLAB 中创建一个简单的矩阵,它只有一行和三个元素。每个元素都应该有一个空格或逗号。
示例
考虑下面提到的元素来创建矩阵。
m=[2, 4, 6]
输出
在 MATLAB 中执行时,它将显示以下内容 -
>>m = [2, 4, 6] m = 2 4 6 >>
当您在 MATLAB 中执行代码时,矩阵的结果将在命令窗口中显示。
多行矩阵
示例
现在让我们创建一个具有多行的矩阵。为此,我们需要用分号 (;) 分隔每一行,如下所示 -
m = [2 4 6; 3 6 9; 4 8 12]
输出
这里2 4 6是第一行,3 6 9是第二行,4 8 12是第三行。矩阵将如下所示 -
m = 2 4 6
3 6 9
4 8 12
现在让我们在 MATLAB 命令提示符下执行相同的操作,如下所示 -
>> m = [2 4 6; 3 6 9; 4 8 12] m = 2 4 6 3 6 9 4 8 12 >>
3x3 矩阵如上所示在 MATLAB 中显示。
除了创建包含您选择的值的矩阵外,您还可以使用内置的 MATLAB 函数 zeros、rand 或 ones 来创建矩阵,如下所示 -
zeros 函数
这将创建一个包含所有零的矩阵,并具有给定的行/列大小。
示例
您可以如下使用 MATLAB zeros 函数 -
m0 = zeros(3,3)
输出
您将获得以下输出 -
>> m0 = zeros(3,3) m0 = 0 0 0 0 0 0 0 0 0 >>
ones 函数
创建的矩阵将以 1 作为值。
示例
您可以如下使用 MATLAB ones 函数 -
m1 = ones(3,3)
输出
您将获得以下输出 -
>> m1 = ones(3,3) m1 = 1 1 1 1 1 1 1 1 1 >>
rand() 函数
rand() 函数允许您为给定的大小创建一个包含随机元素的矩阵。以下是一个示例。
示例
m1 = rand(3,3)
输出
现在让我们在 MATLAB 中执行相同的操作以查看结果。输出如下 -
>> m1 = rand(3,3) m1 = 0.8147 0.9134 0.2785 0.9058 0.6324 0.5469 0.1270 0.0975 0.9575 >>
Matlab矩阵 - 矩阵操作
在本章中,我将介绍如何在 MATLAB 环境中运行矩阵以获取输出。定义矩阵和其他矩阵运算将在接下来的章节中详细讨论。
要在 MATLAB 中获得矩阵输出,将使用 -
- 命令提示符
- 使用 m 文件
使用命令提示符
您可以直接在命令提示符中执行矩阵。以下是一个示例,其中我们有两个矩阵a和b。
操作a+b给出矩阵a和b的和。
操作a-b给出矩阵a和b的差。
命令提示符的输出如下所示 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
>> b = [ 7 5 6 ; 2 0 8; 5 7 1];
>> c = a + b
c =
8 7 9
6 5 14
12 15 10
>> d = a - b
d =
-6 -3 -3
2 5 -2
2 1 8
>>
使用 m 文件
您还可以使用文件编写代码,然后在命令提示符下执行它,如下所示 -
单击“新建脚本”,如下所示 -
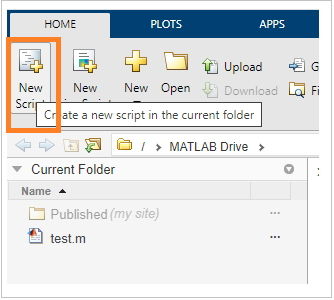
这将打开一个新的未保存文件,如下所示 -

保存文件并在其中编写您的代码
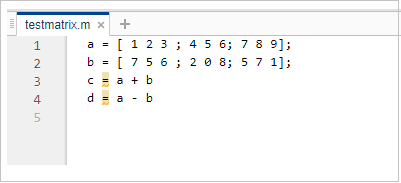
该文件保存为 testmatrix.m。
现在,您可以使用运行按钮或在命令窗口中键入文件名。
输出将在命令窗口中显示,如下所示 -
>> testmatrix
c =
8 7 9
6 5 14
12 15 10
d =
-6 -3 -3
2 5 -2
2 1 8
>>
Matlab矩阵 - 矩阵乘法
考虑两个矩阵 A 和 B。如果 A 是一个m x n矩阵,B 是一个n x p矩阵,则可以将它们相乘以生成一个 m x n 矩阵 C。只有当 A 中的列数 n 等于 B 中的行数 n 时,矩阵乘法才可能。
在矩阵乘法中,第一个矩阵中行的元素与第二个矩阵中相应的列相乘。
结果矩阵 C 中的 (i, j) 位置的每个元素都是第一个矩阵的第 i 行的元素与第二个矩阵的第 j 列中相应元素的乘积之和。
MATLAB 中的矩阵乘法是使用 * 运算符执行的。
示例
考虑 MATLAB 中的以下示例
a = [ 1 2 3; 2 3 4; 1 2 5]; b = [ 2 1 3 ; 5 0 -2; 2 3 -1]; prod = a * b
输出
MATLAB 中的执行将显示以下结果 -
>> a = [ 1 2 3; 2 3 4; 1 2 5];
b = [ 2 1 3 ; 5 0 -2; 2 3 -1];
prod = a * b
prod =
18 10 -4
27 14 -4
22 16 -6
>>
mtimes 函数
您还可以使用mtimes函数来乘以两个给定的矩阵。它是 MATLAB 中可用的内置函数。
示例
考虑以下示例 -
a = [ 1 2 3; 2 3 4; 1 2 5]; b = [ 2 1 3 ; 5 0 -2; 2 3 -1]; test= mtimes(a,b)
输出
在 MATLAB 中执行后,输出如下 -
>> a = [ 1 2 3; 2 3 4; 1 2 5];
b = [ 2 1 3 ; 5 0 -2; 2 3 -1];
test= mtimes(a,b)
test =
18 10 -4
27 14 -4
22 16 -6
>>
Matlab矩阵 - 矩阵加法
要添加两个矩阵,两个操作数矩阵都必须具有相同数量的行和列。
示例
这是一个例子
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = a + b
输出
在 MATLAB 中执行后,结果如下 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a + b
c =
8 7 9
6 5 14
12 15 10
>>
plus() 函数
您还可以使用 plus() 内置函数来添加两个矩阵,如下所示 -
示例
考虑以下使用 plus() 函数添加两个矩阵的示例 -
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = plus(a,b)
输出
MATLAB 中的执行结果如下所示:
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = plus(a,b)
c =
8 7 9
6 5 14
12 15 10
>>
Matlab矩阵 - 矩阵减法
要减去两个矩阵,两个操作数矩阵必须具有相同数量的行和列。
示例
以下是一个示例:
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = a - b
输出
在 MATLAB 中执行后,结果如下 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a - b
c =
-6 -3 -3
2 5 -2
2 1 8
>>
minus() 函数
您还可以使用内置的 minus() 函数来减去两个矩阵。
示例
考虑以下使用 minus() 函数减去两个矩阵的示例:
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = minus(a , b)
输出
您将得到以下结果:
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = minus(a , b)
c =
-6 -3 -3
2 5 -2
2 1 8
>>
Matlab 矩阵 - 行列式
矩阵的行列式是通过使用 MATLAB 的 det 函数计算的。例如,矩阵 A 的行列式由 det(A) 给出。
示例
考虑以下计算矩阵行列式的示例:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = det(a)
输出
在 MATLAB 中执行代码如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5]; test = det(a) test = -2 >>
Matlab矩阵 - 逆矩阵
矩阵 A 的逆表示为 A−1,满足以下关系:
AA−1 = A−1A = 1
矩阵的逆并不总是存在。如果矩阵的行列式为零,则逆不存在,矩阵是奇异的。
MATLAB 中矩阵的逆是使用 inv 函数计算的。矩阵 A 的逆由 inv(A) 给出。
示例
以下是如何计算给定矩阵的逆的示例:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = inv(a)
输出
MATLAB 中的执行结果如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5];
test = inv(a)
test =
-3.5000 2.0000 0.5000
3.0000 -1.0000 -1.0000
-0.5000 0 0.5000
>>
Matlab矩阵 - 迹
迹有助于计算给定矩阵中对角元素的和。
示例
考虑给定的 3x3 矩阵。让我们找出对角元素的和,如下所示:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = trace(a)
输出
MATLAB 中的执行结果如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5] test = trace(a) a = 1 2 3 2 3 4 1 2 5 test = 9 >>
Matlab矩阵 - 秩
矩阵的秩是矩阵中线性无关列的数量。rank() 函数有助于返回给定矩阵的秩。
示例
考虑以下使用 rank() 函数计算矩阵秩的示例:
a = [ 1 2 3; 2 3 4; 1 2 5] test = rank(a)
输出
MATLAB 中执行代码后的输出如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5] test = rank(a) a = 1 2 3 2 3 4 1 2 5 test = 3 >>
Matlab矩阵 - 转置
转置操作交换矩阵中的行和列。它由单引号 (') 表示。
示例
考虑以下示例 -
a = [ 10 12 23 ; 14 8 6; 27 8 9] b = a'
输出
MATLAB 中的执行结果如下:
>> a = [ 10 12 23 ; 14 8 6; 27 8 9] b = a' a = 10 12 23 14 8 6 27 8 9 b = 10 14 27 12 8 8 23 6 9 >>
transpose() 函数
您还可以使用 transpose() 函数来获取矩阵的转置。
示例
考虑以下使用 transpose() 函数的示例:
a = [ 10 12 23 ; 14 8 6; 27 8 9] b = transpose(a)
输出
您将获得以下输出 -
>> a = [ 10 12 23 ; 14 8 6; 27 8 9] b = transpose(a) a = 10 12 23 14 8 6 27 8 9 b = 10 14 27 12 8 8 23 6 9 >>
Matlab 矩阵 - 删除行和列
您可以通过将空方括号 [] 分配给该行或列来删除矩阵的整行或整列。基本上,[] 表示空数组。
示例
例如,让我们删除 a 的第四行,如下所示:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a( 4 , : ) = []
输出
以下是上述代码在 MATLAB 中的执行结果
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a( 4 , : ) = [] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 >>
第四行已删除。它只显示三行。
示例
接下来,让我们删除 a 的第五列,如下所示:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a(: , 5)=[]
输出
让我们看看上述代码在 MATLAB 中的执行结果:
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a(: , 5)=[] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 a = 1 2 3 4 2 3 4 5 3 4 5 6 4 5 6 7 >>