
- MATLAB Simulink 教程
- MATLAB Simulink - 主页
- MATLAB Simulink - 简介
- MATLAB Simulink - 环境设置
- MATLAB Simulink - 启动 Simulink
- MATLAB Simulink - 图块
- MATLAB Simulink - 线
- MATLAB Simulink - 构建和模拟模型
- MATLAB Simulink - 信号处理
- MATLAB Simulink - 向信号添加延迟
- MATLAB Simulink - 数学函数库
- 构建模型并应用 If-else 逻辑
- MATLAB Simulink - 逻辑门模型
- MATLAB Simulink - 正弦波
- MATLAB Simulink - 函数
- MATLAB Simulink - 创建子系统
- MATLAB Simulink - For 循环
- MATLAB Simulink - 导出数据
- MATLAB Simulink - 脚本
- 解决数学方程式
- 一阶微分方程
- MATLAB Simulink 实用资源
- MATLAB Simulink - 快速指南
- MATLAB Simulink - 实用资源
- MATLAB Simulink - 讨论
一阶微分方程
在此,我们将学习如何在 Simulink 中求解一阶微分方程。
我们试图使用 Simulink 求解的一阶微分方程如下 -
dy/dt = 4sin2t - 10y
方程可以通过将 dy/dt 积分到以下项来求解 -
y(t)=∫(4sin2t - 10y(t))dt
以下是针对以上方程构建模型的步骤。
从源函数库选取正弦波并将振幅更改为 4,频率更改为 2。这将给出 4sin2t。
积分器图块将用于显示将输出 y(t) 的 dy/dt。
增益图块将表示 10y。
步骤 1 和 3 的输入将提供给步骤 2。
我们需要示波器图块来观察输出 y(t)。步骤 4 将连接到示波器图块。
让我们在模型中观察上述步骤,如下所示 -
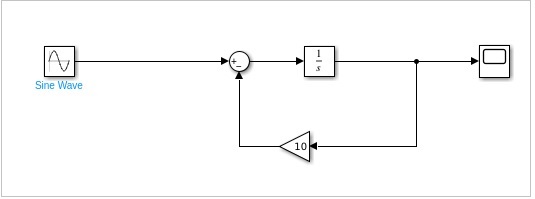
运行图块以查看以下输出 -
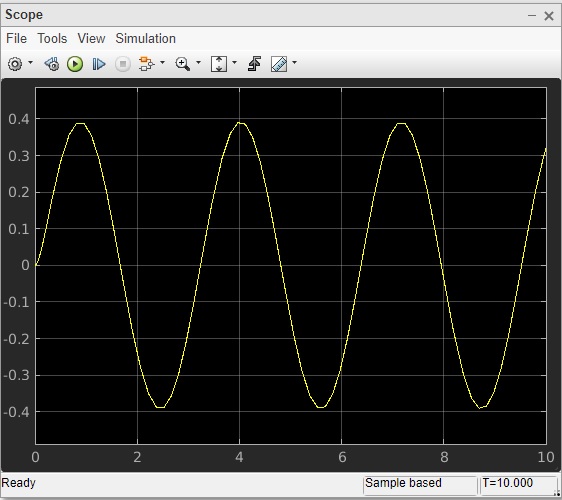
广告