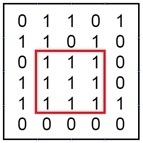
所有元素均为 1 的最大正方形子矩阵
当给出二进制矩阵时,我们的任务是找到所有元素均为 1 的正方形矩阵。
对于这个问题,我们将创建一个辅助大小矩阵,其顺序与给定矩阵相同。此大小矩阵将有助于表示,在每个条目 Size[i, j] 中,具有全部为 1 的正方形矩阵的大小。从该大小矩阵中,我们将获得最大数字以获取最大正方形矩阵的大小。
输入和输出
Input: The binary matrix. 0 1 1 0 1 1 1 0 1 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 0 Output: The largest submatrix with all 1’s.
算法
subMatWithOne(given matrix)
输入 − 主矩阵。
输出 − 显示所有为 1 的正方形矩阵,哪个最大。
Begin define subMat whose order is same as given matrix copy first row and first column of given matrix to subMat for all row i (1 to n), do for all column j (1 to n), do if matrix[i, j] = 1, then subMat[i, j] := 1 + minimum of subMat[i, j-1] and subMat[i-1, j-1] else subMat[i, j] := 0 done done maxSize := subMat[0, 0], iMax := 0 and jMax := 0 for all row i and column j, do if maxSize < subMat[i, j], then maxSize := subMat[i, j] iMax := i, jMax := j done print sub matrix from row = iMax to (iMax - maxSize), and column jMax to (jMax - maxSize) End
示例
#include<iostream>
#define ROW 6
#define COL 5
using namespace std;
int matrix[ROW][COL] = {
{0, 1, 1, 0, 1},
{1, 1, 0, 1, 0},
{0, 1, 1, 1, 0},
{1, 1, 1, 1, 0},
{1, 1, 1, 1, 1},
{0, 0, 0, 0, 0}
};
int min(int a, int b, int c) {
return ((a<b?a:b))?((a<c)?a:c):((b<c)?b:c);
}
void subMatWithOne() {
int subMat[ROW][COL];
int maxSize, iMax, jMax;
for(int i = 0; i < ROW; i++) //copy first row of matrix to sub matrix
subMat[i][0] = matrix[i][0];
for(int j = 0; j < COL; j++) //copy first column of matrix to sub matrix
subMat[0][j] = matrix[0][j];
for(int i = 1; i < ROW; i++) {
for(int j = 1; j < COL; j++) {
if(matrix[i][j] == 1) //find minimum of left, top and diagonal element + 1
subMat[i][j] = min(subMat[i][j-1], subMat[i-1][j], subMat[i-1][j-1]) + 1;
else
subMat[i][j] = 0; //if item is 0, put only 0
}
}
maxSize = subMat[0][0]; iMax = 0; jMax = 0;
for(int i = 0; i < ROW; i++) { //find the order of sub square matrix
for(int j = 0; j < COL; j++) {
if(maxSize < subMat[i][j]) {
maxSize = subMat[i][j];
iMax = i;
jMax = j;
}
}
}
cout << "Subsquare matrix: "<<endl;
for(int i = iMax; i > iMax - maxSize; i--) { //print the submatrix using max size
for(int j = jMax; j > jMax - maxSize; j--) {
cout << matrix[i][j]<<" ";
}
cout << endl;
}
}
int main() {
subMatWithOne();
} 输出
Subsquare matrix: 1 1 1 1 1 1 1 1 1

广告

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP