数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会学
时尚研究
法律研究在 C 程序中打印给定大小的最大和方阵子矩阵。
给定 NxN 的矩阵，查找 MxM 的子矩阵，其中 M<=N 和 M>=1，使矩阵 MxM 中所有元素的总和最大。矩阵 NxN 的输入可以包含零、正和负整数。
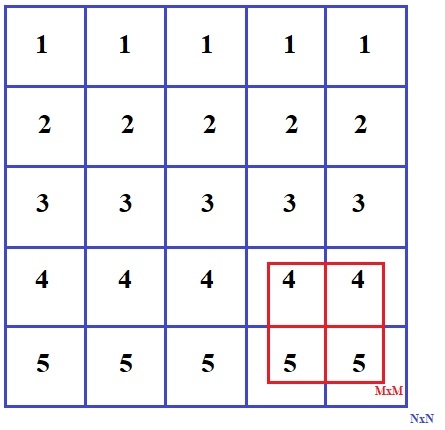
实例
Input:
{{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5} }
Output:
4 4
5 5上述问题可以通过一个简单的解决方案来解决，其中我们可以采用整个矩阵 NxN，然后找出所有可能的矩阵 MxM 并求它们的和，最后打印出具有最大和的矩阵 MxM。这种方法简单，但需要 O(N^2.M^2) 的时间复杂度，因此我们尝试找出一种耗时较少的方法。
算法
Start Step 1 -> Declare Function void matrix(int arr[][size], int k) IF k>size Return Declare int array[size][size] Loop For int j=0 and j<size and j++ Set sum=0 Loop for int i=0 and i<k and i++ Set sum=sum + arr[i][j] End Set array[0][j]=sum Loop For int i=1 and i<size-k+1 and i++ Set sum=sum+(arr[i+k-1]][j]-arr[i-1][j] Set arrayi][j]=sum End Set int maxsum = INT_MIN and *pos = NULL Loop For int i=0 and i<size-k+1 and i++) Set int sum = 0 Loop For int j = 0 and j<k and j++ Set sum += array[i][j] End If sum > maxsum Set maxsum = sum Set pos = &(arr[i][0]) End Loop For int j=1 and j<size-k+1 and j++ Set sum += (array[i][j+k-1] - array[i][j-1]) IF sum > maxsum Set maxsum = sum Set pos = &(arr[i][j]) End End End Loop For int i=0 and i<k and i++ Loop For int j=0 and j<k and j++ Print *(pos + i*size + j) End Print
End Step 2 -> In main() Declare int array[size][size] = {{1, 1, 1, 1, 1}, {2, 2, 2, 2, 2}, {3, 3, 3, 3, 3}, {4, 4, 4, 4, 4}, {5, 5, 5, 5, 5}} Declare int k = 2 Call matrix(array, k) Stop
实例
#include <bits/stdc++.h>
using namespace std;
#define size 5
void matrix(int arr[][size], int k){
if (k > size) return;
int array[size][size];
for (int j=0; j<size; j++){
int sum = 0;
for (int i=0; i<k; i++)
sum += arr[i][j];
array[0][j] = sum;
for (int i=1; i<size-k+1; i++){
sum += (arr[i+k-1][j] - arr[i-1][j]);
array[i][j] = sum;
}
}
int maxsum = INT_MIN, *pos = NULL;
for (int i=0; i<size-k+1; i++){
int sum = 0;
for (int j = 0; j<k; j++)
sum += array[i][j];
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][0]);
}
for (int j=1; j<size-k+1; j++){
sum += (array[i][j+k-1] - array[i][j-1]);
if (sum > maxsum){
maxsum = sum;
pos = &(arr[i][j]);
}
}
}
for (int i=0; i<k; i++){
for (int j=0; j<k; j++)
cout << *(pos + i*size + j) << " ";
cout << endl;
}
}
int main(){
int array[size][size] = {
{1, 1, 1, 1, 1},
{2, 2, 2, 2, 2},
{3, 3, 3, 3, 3},
{4, 4, 4, 4, 4},
{5, 5, 5, 5, 5},
};
int k = 2;
matrix(array, k);
return 0;
}输出
如果我们运行上述程序，它将生成以下输出
4 4 5 5
更新日期：2019 年 8 月 22 日
532 次浏览
广告