平均自由程

---

引言

我们知道，气体中大量的分子被称为粒子。这些粒子在四处随机移动，没有任何排列，由于这种随机运动，它们相互碰撞并改变路径。当难以理解运动粒子的实际路径时，我们使用平均自由程的概念。在平均自由程中，运动粒子指的是原子、光子或分子。

什么是碰撞？

在任何情况下，当两个或多个物体在短时间内施加力而相互碰撞时，称为碰撞。例如，当蜜蜂停落在花瓣上时，它的腿会与花瓣碰撞。碰撞这个术语解释了以下内容：

• 施加力的测量以及碰撞物体运动的变化（速度变化）。

• 这意味着物体在碰撞前的速度大小与碰撞后的速度大小不同。

• 参与碰撞的物体遵循动量守恒定律。因此，每次碰撞都守恒动量。

根据能量（机械能或动能）的守恒情况，碰撞有不同类型。两种类型的碰撞如下：

• 弹性碰撞 − 在碰撞过程中，如果系统的全部动能都守恒，则称为弹性碰撞。它也称为完全弹性碰撞。

• 非弹性碰撞 − 在碰撞过程中，如果一部分动能转化为其他形式的能量，并且系统的总动能不守恒，则称为非弹性碰撞。

弛豫时间

在物理学中，弛豫是指不稳定系统恢复到平衡状态的过程。所有弛豫过程都可以用弛豫时间来指定。

• 导体中两个自由电子连续碰撞之间的时间间隔称为弛豫时间。

• 用字母 𝜏 (tau) 表示。电子的弛豫时间为 10⁻¹⁴ 秒。

• 其公式为 $\mathrm{\tau\:=\:v\frac{n}{e}\:E}$

其中 𝑣 是电子的漂移速度

𝑛 是电子的数量

𝑒 是电子的电荷

𝐸 是电场

• 任何材料的电导率都取决于其弛豫时间。导电性最好的材料将具有更长的弛豫时间。

平均自由程

根据气体动理论，气体分子不断地向各个方向以不同的速度运动，并通过施加力相互碰撞。

• 碰撞后，它们的方向和速度会发生变化。它们不会相互施加力，而只在碰撞时施加力。

• 因此，它们开始以相同的速度在两次连续碰撞之间直线移动。

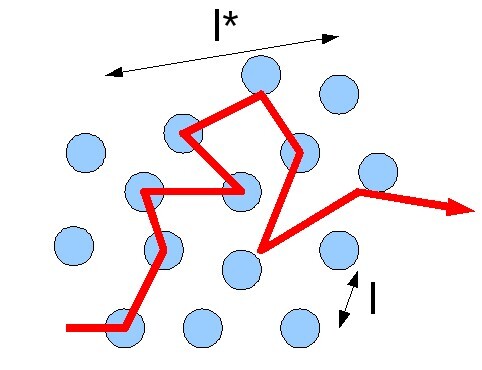
• 如果观察单个运动分子，会发现它具有各种长度的短锯齿形路径。这些分子的短锯齿形路径称为自由程，它们的平均值称为平均自由程。

• 在射线照相中，单能光子束，以及在电子学中，电荷载流子电子具有平均自由程。

让我们假设在房间里移动的球代表运动的分子。球多次撞击房间的墙壁，每次碰撞后，球的方向都会发生变化。球与墙壁之间发生了四次碰撞。在两次连续碰撞之间，球会走出一条特定的路径。这意味着，球走过三条路径，每条路径在四次碰撞之间都有一个确定的距离 d。球的平均自由程是三条路径的平均长度。

因此，$\mathrm{\lambda\:=\:\frac{d_{1}\:+\:d_{2}\:+\:d_{3}}{3}}$

平均自由程的推导

让我们假设理想气体中一个运动的球形分子。气体分子相互碰撞，但我们将研究我们所考虑的运动分子，而气体的其余分子是静止的。

让我们假设运动分子具有直径 d。这个特殊的分子穿过气体，扫出一个短圆柱体，其横截面积为 $\mathrm{\pi\:d^{2}}$

在连续碰撞之间，如果这个分子以速度 v 运动一小段时间 t，它将移动 vt 的距离。现在，如果扫过圆柱体，则得到体积 $\mathrm{\pi\:d^{2}\times\:vd}$。

因此，运动分子的碰撞次数可以通过该体积中存在的点分子数量来获得。

因此，单位体积中的分子数为 $\mathrm{\frac{N}{V}}$

所以，圆柱体中的分子数量是 $\mathrm{\pi\:d^{2}\:vd}\times\:\frac{N}{V}$

平均自由程将如下所示

$$\mathrm{\lambda\:=\:\frac{总时间t内走过的距离}{时间t内的碰撞次数}\:\thickapprox\:\frac{vt}{\pi\:d^{2}vt\frac{N}{V}}\thickapprox\:\frac{1}{\pi\:d^{2}\frac{N}{V}}}$$

推导出的平均自由程方程是近似的，因为在推导的开始，假设只有被研究的分子在运动，而气体的其余分子是静止的。在上式中，由于分子在分母和分子里速度不同（一个是平均速度，一个是相对速度），因此两者之间存在 √2 的差异。

所以，最终方程是

$\mathrm{\lambda\:=\frac{1}{\sqrt{2}\pi\:d^{2}\frac{N}{V}}}$

结论

碰撞是两个或多个物体在短时间内相互碰撞，施加力导致这些物体运动发生变化。碰撞分为弹性碰撞和非弹性碰撞两种类型。弛豫时间是导体中自由电子碰撞之间的时间间隔。用 𝜏 表示。平均自由程是运动分子在连续碰撞之间移动的平均距离。平均自由程方程是 $\mathrm{\lambda\:=\frac{1}{\sqrt{2}\pi\:d^{2}\frac{N}{V}}}$

常见问题解答

1. 写出平均自由程所依赖的因素。

平均自由程取决于

• 分子数量

• 密度

• 分子半径

• 压力、温度

2. 定义相对速度

相对速度是物体相对于另一个物体的相对位置随时间的变化率。

3. 各举一个弹性碰撞和非弹性碰撞的例子。

弹性碰撞的一个例子是原子之间的碰撞，而非弹性碰撞的一个例子是公共汽车撞到树上。

4. 两个物体在非弹性碰撞后如何运动？

在非弹性碰撞中，两个碰撞物体之间没有相应的运动。因此，这些物体作为一个整体一起运动。

5. 写出非弹性碰撞的另一个名称

非弹性碰撞的另一个名称是塑性碰撞。

6. 什么是平均速度？

物体在总时间 t 内走过的总位移称为平均速度。

7. 指出应用于弹性碰撞但不应用于非弹性碰撞的守恒定律。

动能守恒定律应用于弹性碰撞，但不应用于非弹性碰撞。