数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学到达目的地的最小初始点数
从给定网格的左上角开始，需要到达右下角。网格中的每个单元格都包含一个数字，该数字可能是正数或负数。当到达单元格 (i, j) 时，拥有的代币数量可能会随着该单元格的值增加或减少。我们必须找到完成旅程所需的最小初始代币数。
有一些规则：
- 可以向右或向下移动。
- 如果总代币少于 (i, j) 的值，则不能移动到单元格 (i, j)。
- 必须以最小的正点数到达目的地。
输入和输出
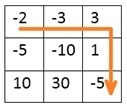
Input: The token for each room as a matrix. -2 -3 3 -5 -10 1 10 30 -5 Output: The minimum token required to start the journey. For this example, the required token is 7.
算法
minInitTokens(matrix)
输入：每个房间的代币矩阵。
输出：从起点到达目的地的最小所需代币数。
Begin define matrix minToken of size same as matrix m := number of rows in matrix n := number of columns in matrix if matrix[m-1, n-1] > 0, then minToken[m-1, n-1] := 0 else minToken[m-1, n-1] := 1 + absolute value of matrix[m-1, n-1] for i := m-2 down to 0, do minToken[i, n-1] := maximum of 1 and (minToken[i+1, n-1]-matrix[i,n-1]) done for j := n-2 down to 0, do minToken[m-1, j] := maximum of 1 and (minToken[m-1, j+1]-matrix[m-1, j]) done for i := m-2 down to 0, do for j := n-2 down to 0, do rem := minimum of minToken[i+1, j] and minToken[i, j+1] minPoint[i, j] := maximum of 1 and (rem – matrix[i,j]) done done return minToken[0, 0] End
示例
#include<iostream>
#include<cmath>
#define ROW 3
#define COL 3
using namespace std;
int tokens[ROW][COL] = {
{-2,-3,3},
{-5,-10,1},
{10,30,-5}
};
int max(int a, int b) {
return (a>b)?a:b;
}
int minInitPoints() {
int minToken[ROW][COL];
int m = ROW, n = COL;
minToken[m-1][n-1] = tokens[m-1][n-1] > 0? 1: abs(tokens[m-1][n-1]) + 1;
for (int i = m-2; i >= 0; i--) //from last row to first row, fill points
minToken[i][n-1] = max(minToken[i+1][n-1] - tokens[i][n-1], 1);
for (int j = n-2; j >= 0; j--) //fill last column to first column, fill points
minToken[m-1][j] = max(minToken[m-1][j+1] - tokens[m-1][j], 1);
for (int i=m-2; i>=0; i--) {
for (int j=n-2; j>=0; j--) {
int remPoint = min(minToken[i+1][j], minToken[i][j+1]); //calculate remaining points
minToken[i][j] = max(remPoint - tokens[i][j], 1);
}
}
return minToken[0][0];
}
int main() {
cout << "Minimum Points Required: " << minInitPoints();
}输出
Minimum Points Required: 7
更新于：2020年6月17日
847 次浏览
广告