使用加法或减法在每一步获得 N 的最小步数

---

从以上问题陈述中，我们的任务是获得在每一步使用加法或减法获得给定数字 N 的最小步数。我们可以理解，我们需要打印我们可以对任何给定整数 N 执行的最小步数以及步骤序列，以从 0 开始通过加或减步数来达到该数字。

在这组问题中，我们可以在每一步从当前位置添加或减去等于步数的数字。例如，我们可以在步骤 1 中添加 1 或 -1。进一步向前移动，我们可以在步骤 2 中添加 2 或 -2，依此类推。我们可以根据情况在每一步添加或减去数字。

问题的核心挑战是我们需要从 0 开始执行最少的步骤才能达到 N。让我们用一个例子更好地理解这个问题。

以下给出的示例将向您说明从 0 开始通过执行所述操作，我们可以用 2 步到达的每个数字。

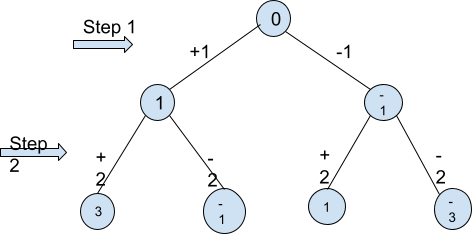
例如，假设我们给定N=1。

输出

Minimum no of steps: 1
Sequence of steps: 1

解释

我们可以通过两种方式到达 1 -

• 在步骤 1 中简单地添加 1 以从 0 移动到 1，这需要 1 步。

• 在步骤 1 中减去 1 以从 0 移动到 -1，然后在步骤 2 中添加 2 以从 -1 移动到 1，这需要 2 步。

由于问题说明我们需要最少的步骤才能到达任何数字 N，因此此输入的期望输出将为 1。

对于，N=3

输出

Minimum no of steps: 2
Sequence of steps: 1 2

解释

我们在步骤 1 中添加 1 以从 0 移动到 1，然后在步骤 2 中添加 2 以从 1 移动到 3。

方法

解决问题的最佳方法是首先确定 N 是正数还是负数。我们必须分别在适当的步数上加或减才能解决问题。

• 如果 N 是正数，请继续添加步数，直到总和超过或等于 N。

• 类似地，如果 N 是负数，请继续减去步数，直到总和超过或等于 N。

• 如果在上述情况下总和等于 N，则返回步数和步骤序列。主要问题是如何处理它超过 N 的情况。

一旦总和超过 N，检查 (sum-N) 是偶数还是奇数。

• 如果 (sum-N) 是偶数，则必须在 (sum-N)/2 步执行减法以达到 N。

  让我们用一个合适的例子更好地理解这种情况。

  对于，N=8

  1+2+3+4=10，它超过了 8。

  由于 10-8=2 是偶数。因此，我们将在 2/2 步执行减法，即

  步骤 1。因此，步骤序列将为-1 2 3 4，达到 N 的最小

  步数将为4。

• 如果 (sum-N) 是奇数，我们首先将确定总和超过数字 N 的前一步是偶数还是奇数。

  如果前一步是奇数，则通过添加下一个步数再执行一步，这将使 (sum-N) 成为偶数，然后执行上述步骤以获得所需的结果。

  例如，N=9

  1+2+3+4=10，超过 9。

  由于 10-9=1 是奇数。下一步是 5，它是一个奇数，因此我们将只通过将 5 添加到总和中执行一步，这将得到 15，使 (sum-N)=6。在步骤 3 执行减法将给出序列1 2 -3 4 5，这是所需的输出。

  让我们假设如果前一步是偶数，在这种情况下，我们需要执行两步，即添加第 i 步并减去第(i+1)步，以使 (sum-N) 成为偶数以获得所需的步骤序列。

  对于 N=5

  1+2+3=6，超过 5。

  由于 (sum-N) =1，因此我们将考虑 su 超过数字 N 时的最后一步。由于它是偶数，我们将执行两步，即第 4 步和第 5 步。我们的任务是使 (sum-N) 成为偶数，因此通过在第 4 步添加并在第 5 步减去，我们可以使 (sum-N) 成为偶数，因为它将从总和中减去 1。由于 (sum-N) 等于 0，我们达到 N。因此，序列为1 2 3 4 -5。

示例

以下是该方法的 C++ 代码 -

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
   vector <int> steps; // for storing the sequence
   int totalSum=0; 
   int temp=0;
   if(n>=0){   // if n is positive then temp will store positive
      temp=1;
   } else {
      temp=-1;  // n is negative then temp will store negative
   }
   n=abs(n);
   int step=0;
   for(step=1;totalSum<n;step++){  // for storing the steps till sum is not greater than n
      steps.push_back(temp*step);
   
      totalSum=totalSum+step;
   }
   if(totalSum>temp*n) {  //when sum greater than n 
      if(step%2==0) {   //when step is even 
         totalSum=totalSum-n; 
         if((totalSum)%2!=0) { // when totalSum-n is odd
            steps.push_back(temp*step);  //store the addition of next step 
            steps.push_back((temp*-1)*(step+1));  // store the subtraction of next step 
            totalSum--;  //make totalSum even
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1; 
		} else {        //when step is odd
         totalSum=totalSum-n;
         if((totalSum)%2!=0)  {  // when totalSum-n is odd 
            steps.push_back(temp*step);   //store the next addition value 
            totalSum+=step; 
            step++;
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1;
   
      }
   }
   //print the minimum number of steps taken 
   cout<<"The minimum number of steps : "<<steps.size()<<endl;
   //print the steps is stored in vector
      cout<<"Sequence of steps : ";
   for(int i=0;i<steps.size();i++){
      cout<<steps[i]<<" ";
   }
   
}
int main(){
   int m=17;
   minimumStep(m);
   
   return 0;
}

输出

The minimum number of steps : 6
Sequence of steps : 1 -2 3 4 5 6

时间复杂度：O(sqrt(N))

空间复杂度：O(sqrt(N))

结论

在本文中，我们试图解释找到通过在每一步添加或减去来达到 N 的最小步数并打印序列的方法。我希望本文能帮助您更好地学习这个概念。