数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究信号与系统：信号的加法和减法
连续时间信号的加法和减法
两个连续时间信号𝑥1(𝑡)和𝑥2(𝑡)的和可以通过在每个时刻将它们的值相加得到。类似地，两个连续时间信号𝑥1(𝑡)和𝑥2(𝑡)的差可以通过在每个时刻从另一个信号（例如𝑥1(𝑡)）中减去一个信号（例如𝑥2(𝑡)）的值得到。
信号的加法
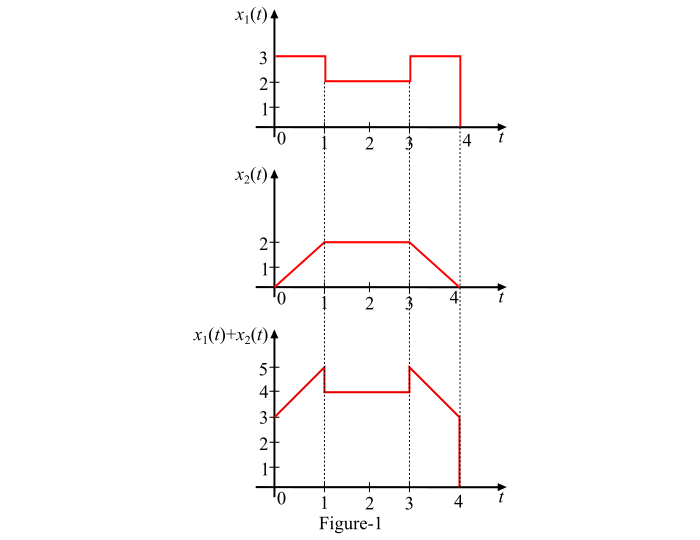
如图 1 所示，设有两个连续时间信号𝑥1(𝑡)和𝑥2(𝑡)。这两个信号的和𝑥1(𝑡) + 𝑥2(𝑡)也如图 1 所示。
说明
这两个信号的和可以通过考虑不同的时间间隔得到，如下所示：
对于0 ≤ 𝒕 ≤ 1− 𝑥1(𝑡) = 3，而𝑥2(𝑡)从 0 线性增加到 2。因此，和[即，𝑥1(𝑡) + 𝑥2(𝑡)]也将从（3 + 0 = 3）线性增加到（3 + 2 = 5）。
对于1 ≤ 𝒕 ≤ 3− 𝑥1(𝑡) = 2，而𝑥2(𝑡) = 2，因此
𝑥1(𝑡) +𝑥2(𝑡) = 2 + 2 = 4
对于3≤ 𝒕 ≤ 4− 𝑥1(𝑡) = 3，而𝑥2(𝑡)从 2 线性减小到 0。因此，信号的和也将从（3 + 2 = 5）线性下降到（3 + 0 = 3）。
信号的减法
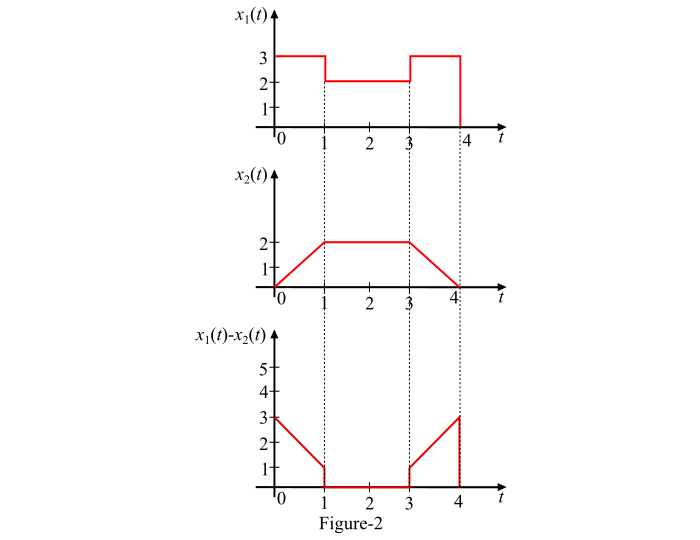
图 2 显示了两个连续时间信号𝑥1(𝑡)和𝑥2(𝑡)的减法[𝑥1(𝑡) − 𝑥2(𝑡)]。
说明
可以通过考虑不同的时间间隔得到两个连续时间信号𝑥1(𝑡)和𝑥2(𝑡)的差，如下所示：
对于0 ≤ 𝒕 ≤ 1−𝑥1(𝑡) = 3，而𝑥2(𝑡)从 0 线性增加到 2。因此，差[𝑥1(𝑡) −𝑥2(𝑡)]从（3 – 0 = 3）线性下降到（3 – 2 = 1）。
对于1 ≤ 𝒕 ≤ 3− 𝑥1(𝑡) = 2，而𝑥2(𝑡) = 2，因此
𝑥1(𝑡) − 𝑥2(𝑡) = 2 − 2 = 0
对于3≤ 𝒕 ≤ 4− 𝑥1(𝑡) = 3，而𝑥2(𝑡)从 2 线性减小到 0。因此，信号的差将从（3 – 2 = 1）线性上升到（3 – 0 = 3）。
离散时间信号的加法和减法
在离散时间情况下，两个序列𝑥1(𝑛)和𝑥2(𝑛)的和可以通过将相应的样本值相加得到。类似地，两个序列𝑥1(𝑛)和𝑥2(𝑛)的差可以通过从另一个信号的对应样本中减去一个信号的每个样本得到。
假设给出两个离散时间序列，如下所示：
𝑥1(𝑛) = {2, 1, 3, 5, 2}
𝑥2(𝑛) = {1, 4, 2, 1, −3}
然后，离散时间信号的加法为：
𝑥1(𝑛) + 𝑥2(𝑛) = {2 + 1, 1 + 4, 3 + 2, 5 + 1, 2 − 3} = {3, 5, 5, 6, −1}
类似地，离散时间信号的减法为：
𝑥1(𝑛) - 𝑥2(𝑛) = {2 − 1, 1 − 4, 3 − 2, 5 − 1, 2 + 3} = {1, −3, 1, 4, 5}
8K+ 次浏览
