数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学信号与系统：奇偶信号
偶信号
关于垂直轴或时间原点对称的信号称为**偶信号**或**偶函数**。因此，偶信号也称为**对称信号**。余弦波是偶信号的一个例子。
连续时间偶信号
如果满足以下条件，则连续时间信号 x(t) 称为偶信号或对称信号：
𝑥(𝑡) = 𝑥(−𝑡); 对于 − ∞ < 𝑡 < ∞
图1显示了一些连续时间偶信号的示例。
离散时间偶信号
如果满足以下条件，则离散时间信号 x(n) 称为偶信号或对称信号：
𝑥(𝑛) = 𝑥(−𝑛); 对于 − ∞ < 𝑛 < ∞
图2显示了一些离散时间偶信号的示例。
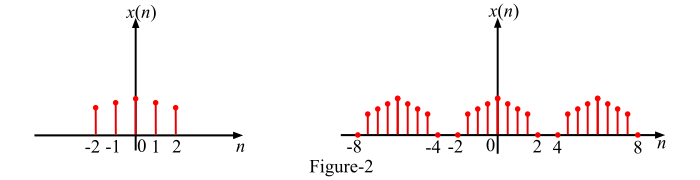
偶信号的特性
偶信号的特性如下：
- 偶信号关于垂直轴对称。
- 偶信号在时间 (t) 处的数值与在时间 (-t) 处的数值相同。
- 偶信号与其关于原点的反射相同。
- 偶信号下的面积是其单侧面积的两倍。
奇信号
关于垂直轴反对称的信号称为奇信号或**奇函数**。因此，奇信号也称为**反对称信号**。正弦波是奇信号的一个例子。
连续时间奇信号
如果满足以下条件，则连续时间信号 x(t) 称为奇信号或反对称信号：
𝑥(−𝑡) = −𝑥(𝑡); 对于 − ∞ < 𝑡 < ∞
图3显示了一些连续时间奇信号或反对称信号的示例。
离散时间奇信号
如果满足以下条件，则离散时间信号 x(n) 称为奇信号或反对称信号：
𝑥(−𝑛) = −𝑥(𝑛); 对于 − ∞ < 𝑛 < ∞
图4显示了一些离散时间奇信号的示例。
奇信号的特性
奇信号的特性如下：
奇信号关于原点反对称。
奇信号在时间 (t) 处的数值在其时间 (-t) 处的数值的负数，对于所有 t，即 −∞ < 𝑡 < ∞。
为了满足 𝑥(0) = −𝑥(0)，奇信号在时间 t = 0 处必须为零。
奇信号下的面积始终为零。
**注意** – 如果连续时间信号不满足偶信号和奇信号的条件，则该信号既不是偶信号也不是奇信号。图5显示了此类信号 (既不是偶信号也不是奇信号) 的一些示例。
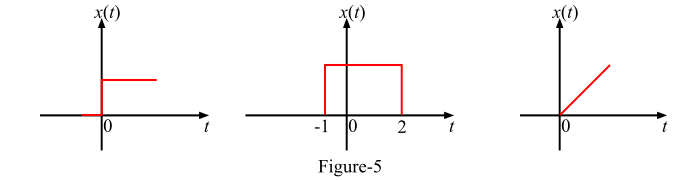
数值示例
确定信号是偶信号还是奇信号。
𝑥(𝑡) = 𝑒−5𝑡
𝑥(𝑡) = sin 2𝑡
𝑥(𝑡) = cos 5𝑡
解答
给定信号为：
𝑥(𝑡) = 𝑒−5𝑡
𝑥(−𝑡) = 𝑒5𝑡
−𝑥(𝑡) = −𝑒−5𝑡
很明显，𝑥(𝑡) ≠ 𝑥(−𝑡) 且 𝑥(−𝑡) ≠ −𝑥(𝑡)，因此给定信号既不是偶信号也不是奇信号。
给定信号为：
𝑥(𝑡) = sin 2𝑡
𝑥(−𝑡) = −sin 2𝑡
−𝑥(𝑡) = −sin 2𝑡
因此，𝑥(𝑡) ≠ 𝑥(−𝑡)；但 𝑥(−𝑡) = −𝑥(𝑡)，因此给定信号是奇信号。
给定信号为：
𝑥(𝑡) = cos 5𝑡
𝑥(−𝑡) = cos 5𝑡
−𝑥(𝑡) = −cos 5𝑡
因此，𝑥(𝑡) = 𝑥(−𝑡) 且 𝑥(−𝑡) ≠ −𝑥(𝑡)，因此给定信号是偶信号。
34K+ 次浏览
