数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学信号与系统——什么是偶对称性？
波形对称性的重要性
如果周期信号𝑥(𝑡)具有一定的对称性，则一些三角傅里叶级数系数可能变为零，从而简化系数的计算。
偶对称或镜像对称
当周期函数关于垂直轴对称时，则称其具有**偶对称性**或**镜像对称性**。偶对称性也称为反射对称性。数学上，如果周期函数x(t)满足：
$$\mathrm{𝑥(𝑡) = 𝑥(−𝑡)\:\:\:\:\:\: ...(1)}$$
图中显示了一些具有偶对称性的函数示例。偶函数总是关于垂直轴对称的。
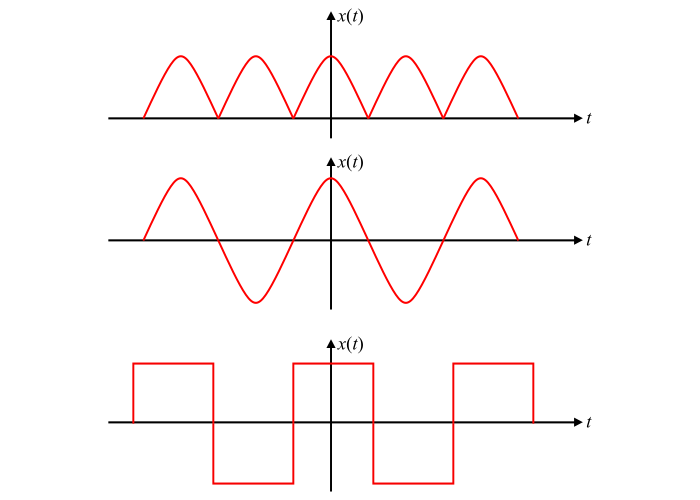
解释
我们知道，任何周期信号𝑥(𝑡)都可以分解成偶分量和奇分量，即：
$$\mathrm{𝑥(𝑡) = 𝑥_{𝑒}(𝑡) + 𝑥_{𝑜}(𝑡) … (2)}$$
如果函数𝑥(𝑡)是偶函数，则：
$$\mathrm{𝑥_{𝑜}(𝑡) = 0}$$
$$\mathrm{\therefore\:𝑥(𝑡) = 𝑥_{𝑒}(𝑡)\:\:\:\:\:\: … (3)}$$
因此，三角傅里叶级数系数由下式给出：
$$\mathrm{𝑎_{0}\: =\:\frac{1}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥(𝑡)\: dt\:=\: \frac{1}{𝑇}\:\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡)\: dt}$$
$$\mathrm{⇒𝑎_{0}\: =\:\frac{1}{𝑇}(2\int_{0}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \: dt)\:=\:\frac{2}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \: dt}$$
$$\mathrm{\therefore 𝑎_{0}\: =\:\frac{2}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \: dt\:\:\:.....(4)}$$
系数𝑎𝑛由下式给出：
$$\mathrm{𝑎_{𝑛}\: =\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥(𝑡) \cos\:n\omega_{0}t\: dt\:=\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \cos\:n\omega_{0}t\: dt}$$
$$\mathrm{𝑎_{𝑛}\: =\:\frac{2}{𝑇}(2\int_{0}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \cos\:n\omega_{0}t\: dt)}$$
$$\mathrm{\therefore 𝑎_{𝑛}\: =\:\frac{4}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \cos\:n\omega_{0}t\: dt\:\:\:.....(5)}$$
系数𝑏𝑛由下式给出：
$$\mathrm{𝑏_{𝑛} =\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \sin\:n\omega_{0}t\: dt}$$
由于函数(𝑥𝑒(𝑡) sin 𝑛𝜔0𝑡)是奇函数。
$$\mathrm{\therefore 𝑏_{𝑛}\:=\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \sin\:n\omega_{0}t\: dt\:= 0\:\:\:.....(6)}$$
因此，偶周期函数的傅里叶级数展开式只包含常数项和余弦项。此外，当函数存在偶对称或镜像对称时，该函数的三角傅里叶级数系数由公式(4)、(5)和(6)给出。
从以上讨论可以看出，当函数存在偶对称性时，三角傅里叶系数𝑏𝑛变为零，从而简化了计算。
偶函数的性质
- 两个或多个偶函数之和始终为偶函数。
- 两个偶函数的乘积始终为偶函数。
- 当向偶函数添加常数时，函数的偶性仍然保持。
浏览量2K+
