数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究信号与系统 – 什么是半波对称性？
波形对称性的重要性
如果一个周期信号 $x(t)$ 具有某种类型的对称性，则一些三角傅里叶级数系数可能会变为零，因此系数的计算变得简单。
半波对称性
如果一个周期函数 $x(t)$ 满足以下条件，则称其具有半波对称性：
$$\mathrm{x(t)=-x\left ( t ± \frac{T}{2}\right )… (1)}$$
其中，$T$ 是函数的周期。
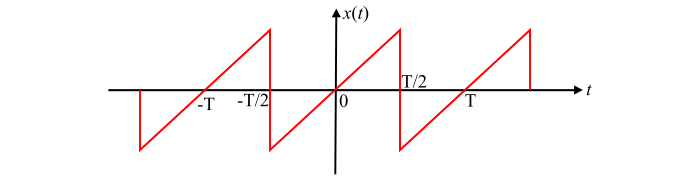
具有半波对称性的周期函数 $x(t)$ 如图所示。可以看出，此函数既不是纯偶函数也不是纯奇函数。对于此类函数，傅里叶展开的直流分量为零，即 $a_{0}=0$。此外，此类函数的傅里叶展开仅包含奇次谐波分量，即 $\omega_{0},3\omega_{0},5\omega_{0},...$ 等。
由于具有半波对称性的周期函数 $x(t)$ 仅包含奇次谐波项。因此，当 n 为偶数时，$a_{n}=b_{n}=0$。
当 n 为奇数时，系数 $a_{n}$ 和 $b_{n}$ 可以如下确定：
$$\mathrm{a_{n}=\frac{2}{T}\int_{0}^{T}x(t)cos\:n\omega_{0}t\:dt}$$
$$\mathrm{\Rightarrow\:a_{n}=\frac{2}{T}\left [ \int_{0}^{T/2} x(t)cos\:n\omega_{0}t\:dt+\int_{T/2}^{T} x(t)cos\:n\omega_{0}t\:dt\right ]}$$
在第二个积分项中将变量从 $t$ 替换为 $(t+\frac{T}{2})$，我们有：
$$\mathrm{a_{n}=\frac{2}{T}\left [ \int_{0}^{T/2} x(t)cos\:n\omega_{0}t\:dt+ \int_{0}^{T/2} x(t+\frac{T}{2})cos\:n\omega_{0}(t+\frac{T}{2})dt\right ]}$$
根据半波对称性的定义，即 $x(t)=-x(t ± \frac{T}{2})$，我们有：
$$\mathrm{a_{n}=\frac{2}{T}\int_{0}^{T/2}[x(t)\:cos\:n\omega_{0}t-x(t)\:cos\:n\omega_{0}t\:cos\:n\pi]dt… (2)}$$
因此，具有半波对称性的函数的傅里叶级数系数 $a_{n}$ 可以定义为：
$$\mathrm{a_{n}=\begin{cases}0; & 当n为偶数时\\frac{4}{T}\int_{0}^{T/2}\:x(t)\:cos\:n\omega_{0}t\:dt\:;& 当n为奇数时\end{cases}}$$
类似地，系数 $b_{n}$ 由下式给出：
$$\mathrm{b_{n}=\begin{cases}0; & 当n为偶数时\\frac{4}{T}\int_{0}^{T/2}\:x(t)\:sin\:n\omega_{0}t\:dt\:;& 当n为奇数时\end{cases}}$$
9K+ 次浏览
