数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究信号与系统 – 希尔伯特变换是什么？
希尔伯特变换
当信号所有正频率谱分量的相位角移位 (-90°)，所有负频率谱分量的相位角移位 (+90°) 时，得到的时域函数称为给定信号的希尔伯特变换。
在信号的希尔伯特变换中，信号的幅度谱不变，只有信号的相位谱发生变化。此外，信号的希尔伯特变换不改变信号的定义域。
假设一个信号 x(t) 的傅里叶变换为 X(ω)。x(t) 的希尔伯特变换通过 x(t) 与 (1/πt) 的卷积得到，即：
$$\mathrm{\hat{x}(t)=x(t)*(\frac{1}{\Pi\:t})}$$
$$\mathrm{\Longrightarrow\hat{x}(t)=\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{x(\tau)}{t-\tau}d\tau}$$
此外，
$$\mathrm{\hat{x}(t)=\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{x(t-\tau)}{\tau}d\tau}$$
这表明信号 x(t) 的希尔伯特变换是一个线性运算。这个希尔伯特变换的定义适用于所有可进行傅里叶变换的信号。
逆希尔伯特变换
从 $\hat{x}(t)$ 中恢复原始信号 x(t) 的过程称为逆希尔伯特变换。在数学上，它定义为：
$$\mathrm{x(t)=-\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{\hat{x}(\tau)}{t-\tau}d\tau}$$
函数 x(t) 和 $\hat{x}(t)$ 的方程一起称为希尔伯特变换对。
解释
由于信号 x(t) 的希尔伯特变换 $\hat{x}(t)$ 是通过 x(t) 与 (1/πt) 的卷积得到的。因此，根据傅里叶变换的卷积性质，两个时域函数的卷积可以转化为它们在频域中的傅里叶变换的乘积。
信号 (1/πt) 的傅里叶变换定义为：
$$\mathrm{F=\left[\frac{1}{\pi\:t}\right]=-j\:sgn(\omega)}$$
其中，sgn(ω) 是频域中的符号函数，定义为
$$\mathrm{sgn(\omega)=\left\{\begin{matrix} 1;\: \omega >0 \ -1;\: \omega <0 \ \end{matrix}\right.}$$
现在，$\hat{x}(t)$ 的傅里叶变换 $\hat{X}(ω)$ 由下式给出：
$$\mathrm{F[\hat{x}(t)]=\hat{X}(\omega)=-j\:sgn(\omega).X(\omega)}$$
这意味着，
$$\mathrm{\hat{X}(\omega)=\left\{\begin{matrix} -jX(\omega);\:\:\omega>0 \ jX(\omega) ;\:\:\omega<0 \end{matrix}\right.}$$
这个表达式表明，信号 x(t) 的希尔伯特变换 $\hat{x}(t)$ 可以通过使 x(t) 通过一个传递函数为 [-j\:sgn(ω)] 的线性器件来获得。这个线性器件可以被认为是为输入信号的所有正频率产生 (-90°) 相移，为所有负频率产生 (+90°) 相移的器件。
此外，信号中所有频率谱分量的幅度不受信号通过器件传输的影响，即：
$$\mathrm{\left|\hat{X}(\omega)\right |=\left |X(\omega)\right|}$$
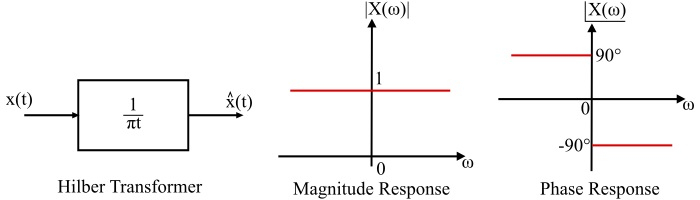
这种理想的器件称为希尔伯特变换器。希尔伯特变换器可以看作是一个理想的全通 90° 移相器。希尔伯特变换器是非因果的，即它在物理上是不可实现的。
图中显示了希尔伯特变换器及其幅度响应和相位响应的图形表示。
重要 - 低通信号和高通信号乘积的希尔伯特变换等于低通信号与高通信号的希尔伯特变换的乘积。因此，如果 x(t) 是低通信号，y(t) 是高通信号，则：
$$\mathrm{\widehat{x(t).y(t)}=x(t).\widehat{y(t)}}$$
希尔伯特变换的应用
希尔伯特变换主要应用于信号处理、信号分析与合成以及滤波器设计等领域。希尔伯特变换的一些主要应用如下：
希尔伯特变换用于表示带通信号。
希尔伯特变换用于在单边带 (SSB) 调制系统中实现相位选择性。
希尔伯特变换还用于关联线性通信信道的增益和相位特性以及最小相位类型的滤波器。
数值例子
求给定信号的希尔伯特变换：
$$\mathrm{x(t)=sin\:\omega_{0}t}$$
解决方案
给定信号为：
$$\mathrm{x(t)=sin\:\omega_{0}t}$$
根据傅里叶变换的定义，我们有：
$$\mathrm{F[sin\omega_{0}t]=X(\omega)=-j\pi[\delta(\omega-\omega_{0})-\delta(\omega+\omega_{0})]}$$
此外，x(t) 的希尔伯特变换的傅里叶变换为
$$\mathrm{F[\hat{x}(t)]=\hat{X}(\omega)=-j\:sgn(\omega).X(\omega)}$$
$$\mathrm{\therefore\hat{X}(\omega)=\left \{ -j\:sgn(\omega) \right \}\left \{-j\pi [\delta (\omega -\omega_{0})-\delta (\omega +\omega_{0})] \right \}}$$
$$\mathrm{\Longrightarrow\hat{X}(\omega)=-\pi [\delta (\omega -\omega_{0})-\delta (\omega +\omega_{0})]sgn(\omega)}$$
$$\mathrm{\Longrightarrow\hat{X}(\omega)=-\pi [\delta (\omega -\omega_{0})+\delta (\omega +\omega_{0})]}$$
因此，给定信号的希尔伯特变换为
$$\mathrm{\hat{x}(t)=F^{-1}\left \{-\pi[\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})] \right \}=-cos\omega_{0}t}$$
或者，它也可以表示为
$$\mathrm{\widehat{sin\omega_{0}t}=-cos\omega_{0}t}$$
7K+ 次查看
