信号与系统 – 整流函数的拉普拉斯变换是什么？

---

拉普拉斯变换

拉普拉斯变换是一种数学工具，用于将时域中的微分方程转换为频域或s域中的代数方程。

数学上，如果$\mathrm{\mathit{x\left ( t \right )}}$是时域函数，则其拉普拉斯变换定义为−

$$\mathrm{\mathit{L\left [ x\left ( t \right ) \right ]\mathrm{\mathrm{=}}X\left ( s \right )\mathrm{\mathrm{=}}\int_{-\infty }^{\infty }x\left ( t \right )e^{-st}\:dt}}$$

全波整流正弦波函数的拉普拉斯变换

全波整流正弦波函数如图 1 所示，其表达式为：

$$\mathrm{\mathit{x\left ( t \right )=\mathrm{sin}\: \omega t;\; \; \mathrm{for\: 0}< \mathit{t}< \frac{\pi }{\omega }}}$$

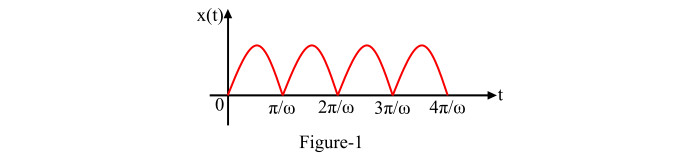
全波整流正弦波函数$\mathrm{\mathit{x\left ( t \right )}}$是周期函数，周期为（𝜋⁄𝜔）。因此，利用拉普拉斯变换的周期性性质$\mathrm{\mathit{\left [\mathrm{ie.,} L\left [ x\left ( t \right ) \right ] = \left [ \mathrm{1}-e^{-sT} \right ]^{-\mathrm{1}}\int_{\mathrm{0}}^{T}x\left ( t \right )e^{-st}dt \right ] }}$，得到：

$$\mathrm{\mathit{X\left ( s \right )\mathrm{=}L\left [ x\left ( t \right ) \right ]\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( s\pi /\omega \right )} \right ]}\int_{\mathrm{0}}^{\left ( \pi /\omega \right )}\mathrm{sin}\mathit{\left (\omega t \right )}e^{-st}dt}}$$

求解右侧积分，得到：

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( s\pi /\omega \right )} \right ]}\left [ \frac{e^{-st}\left ( -s\: \mathrm{sin}\omega t-\omega \: \mathrm{cos}\omega t \right )}{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}} \right ]_{\mathrm{0}}^{\left ( \pi /\omega \right ) }}}$$

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( s\pi /\omega \right )} \right ]}\left [ \frac{\left ( \omega e^{-\left ( s\pi /\omega \right )}\mathrm{\: +\: }\omega \right )}{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}} \right ]\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\left [ \frac{\mathrm{1}\mathrm{\: +\: }e^{-\left ( s\pi /\omega \right )}}{\mathrm{1}-e^{-\left ( s\pi /\omega \right )}} \right ]}}$$

现在，在上述表达式的右侧代入$\mathrm{\mathit{\mathrm{1}\mathrm{=}\left [e^{\left ( s\pi /\mathrm{2}\omega \right )}/e^{\left ( s\pi /\mathrm{2}\omega \right )} \right ]}}$，得到：

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\left [ \frac{e^{\left ( s\pi /\mathrm{2}\omega \right )}\mathrm{\: +\: }e^{-\left ( s\pi /\mathrm{2}\omega \right )}}{e^{\left ( s\pi /\mathrm{2}\omega \right )}-e^{-\left ( s\pi /\mathrm{2}\omega \right )}} \right ]\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\left [ \frac{\mathrm{cosh}\left ( s\pi /\mathrm{2}\omega \right )}{\mathrm{sinh}\left ( s\pi /\mathrm{2}\omega \right )} \right ]}}$$

$$\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}L\left [ \mathrm{sin\: \omega t} \right ]\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\mathrm{coth}\left ( \frac{s\pi }{\mathrm{2}\omega } \right )}}$$

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

半波整流正弦波函数的拉普拉斯变换

半波整流正弦波函数如图 2 所示，其表达式为：

$$\mathrm{\mathit{x\left ( t \right )\mathrm{=} \left\{\begin{matrix} \mathrm{sin}\: \omega t;\;\; \mathrm{for\: 0}< t< \frac{\pi }{\omega }\ \mathrm{0;\;\; for\:} \frac{\pi }{\omega } < t<\frac{\mathrm{2}\pi }{\omega } \ \end{matrix}\right. }}$$

半波整流正弦波函数$\mathrm{\mathit{x\left ( t \right )}}$是周期函数，周期为（2𝜋⁄𝜔）。因此，利用拉普拉斯变换的周期性性质$\mathrm{\mathit{\left [\mathrm{ie.,} L\left [ x\left ( t \right ) \right ] \mathrm{=} \left [ \mathrm{1}-e^{-sT} \right ]^{-\mathrm{1}}\int_{\mathrm{0}}^{T}x\left ( t \right )e^{-st}dt \right ] }}$，得到：

$$\mathrm{\mathit{X\left ( s \right )\mathrm{=}L\left [ x\left ( t \right ) \right ]\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( \mathrm{2}\pi s /\omega \right )} \right ]}\left [ \int_{\mathrm{0}}^{\left ( \pi /\omega \right )}\mathrm{sin}\mathit{\left (\omega t \right )}e^{-st}dt \mathrm{\: +\: } \mathrm{0} \right ]}}$$

求解右侧积分，得到：

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( \mathrm{2}\pi s /\omega \right )} \right ]}\left [ \frac{e^{-st}\left ( -s\: \mathrm{sin}\: \omega t-\omega \: \mathrm{cos}\: \omega t \right )}{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}} \right ]_{\mathrm{0}}^{\left ( \pi /\omega \right ) }}}$$

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{\left [ \mathrm{1}-e^{-\left ( \mathrm{2}\pi s /\omega \right )} \right ]}\left [ \frac{\left ( \omega e^{-\left ( s\pi /\omega \right )}\mathrm{\: +\: }\omega \right )}{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}} \right ]\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\left [ \frac{\mathrm{1}\mathrm{\: +\: }e^{-\left ( s\pi /\omega \right )}}{\mathrm{1}-e^{-\left ( \mathrm{2}\pi s /\omega \right )}} \right ]}}$$

$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\omega }{s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}}}\left\{\frac{\mathrm{1}\mathrm{\: +\: }e^{-\left ( s\pi /\omega \right )}}{\left [ \mathrm{1}-e^{-\left ( s \pi /\omega \right )} \right ]\left [ \mathrm{1}\mathrm{\: +\: }e^{-\left ( s \pi/\omega \right )} \right ]} \right\}}}$$

$$\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}L\left [ \mathrm{sin\: \omega t} \right ]\mathrm{=}\frac{\omega }{\left ( s^{\mathrm{2}}\mathrm{\: +\: }\omega ^{\mathrm{2}} \right )\left ( \mathrm{1}-e^{-s\pi /\omega } \right )}}}$$