信号与系统 – 奇对称性是什么？

波形对称性的重要性

如果周期信号 $x(t)$ 具有某种类型的对称性，则一些三角傅里叶级数系数可能变为零，因此系数的计算变得简单。

奇对称或旋转对称

当周期函数 $x(t)$ 关于垂直轴反对称时，则称该函数具有**奇对称性**或**旋转对称性**。

在数学上，如果函数 $x(t)$ 满足以下条件，则称其具有奇对称性：

$$\mathrm{x(t)=-x(-t)… (1)}$$

图中显示了一些具有奇对称性的函数。很明显，奇对称函数总是关于垂直轴反对称的。

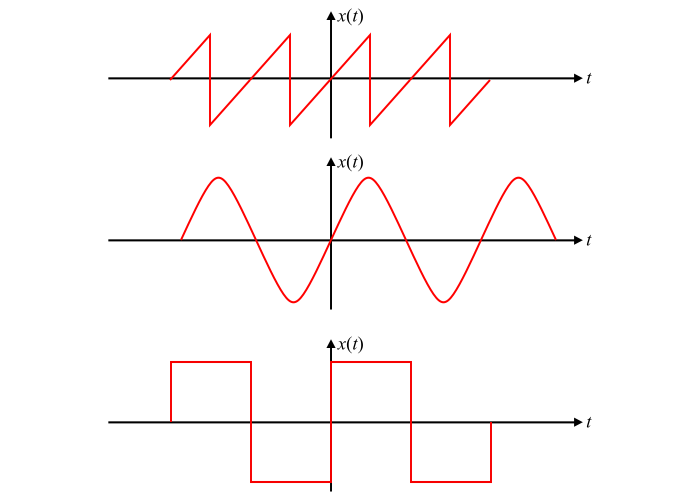
解释

众所周知，任何周期信号 $x(t)$ 都可以分解成偶数和奇数分量，即：

$$\mathrm{x(t)=x_{e}(t)+x_{0}(t)… (2)}$$

如果函数 $x(t)$ 是奇函数，则：

$$\mathrm{x_{e}(t)=0}$$

$$\mathrm{\therefore\:x(t)=x_{0}(t)… (3)}$$

函数的三角傅里叶系数可以如下计算：

系数 $a_{0}$ 由下式给出：

$$\mathrm{a_{0}=\frac{1}{T} \int_{−T/2}^{T/2}x(t)\:dt=\frac{1}{T}\int_{−T/2}^{T/2}x_{0}(t)\:dt}$$

对于奇函数，曲线在一个周期内的面积为零，即：

$$\mathrm{\int_{−T/2}^{T/2}x_{0}(t)\:dt=0}$$

$$\mathrm{\therefore\:a_{0}=0… (4)}$$

系数 $a_{n}$ 由下式给出：

$$\mathrm{a_{n}=\frac{2}{T} \int_{−T/2}^{T/2}x(t)cos\:n\omega_{0} t\:dt}$$

$$\mathrm{\Rightarrow\:a_{n}=\frac{2}{T} \int_{−T/2}^{T/2}x_{0}(t)cos\:n\omega_{0} t\:dt}$$

由于函数 $(x_{0}(t)\:cos\:n\omega_{0𝑡}t)$ 是奇函数，因此其在一个完整周期内的积分值为零。

$$\mathrm{\therefore\:a_{n}=0… (5)}$$

而系数 $b_{n}$ 由下式给出：

$$\mathrm{b_{n}=\frac{2}{T}\int_{−T/2}^{T/2}x(t)sin\:n\omega_{0}t\:dt}$$

$$\mathrm{\Rightarrow\:b_{n}=\frac{2}{T}\int_{−T/2}^{T/2}x_{0}(t)sin\:n\omega_{0}t\:dt=\frac{2}{T}\left ( \int_{0}^{T/2}x_{0}(t)sin\:n\omega_{0}t\:dt \right )}$$

$$\mathrm{\therefore\:b_{n}=\frac{4}{T}\int_{0}^{T/2}x(t)sin\:n\omega_{0}t\:dt… (6)}$$

因此，奇周期函数的傅里叶级数展开式仅包含正弦项。当函数存在奇对称或旋转对称时，函数的三角傅里叶级数系数由公式 (4)、(5) 和 (6) 给出。

奇函数的性质

• 两个或多个奇函数的和始终为奇函数。

• 两个奇函数的积为偶函数。

• 当向奇函数添加常数时，函数的奇特性将被消除。

Manish Kumar Saini

更新于: 2021-12-07

2K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习