数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学信号与系统：实指数信号与复指数信号
实指数信号
指数信号或指数函数是一个字面意义上表示指数递增或递减序列的函数。
连续时间实指数信号
在每一个时刻都定义的实指数信号称为连续时间实指数信号。连续时间实指数信号定义如下：
𝑥(𝑡) = 𝐴𝑒𝛼𝑡
其中，A 和 𝛼 都是实数。这里参数 A 是在 t = 0 时测量的指数信号的幅度，参数 𝛼 可以是正数或负数。
根据 𝛼 的值，我们得到不同的指数信号：
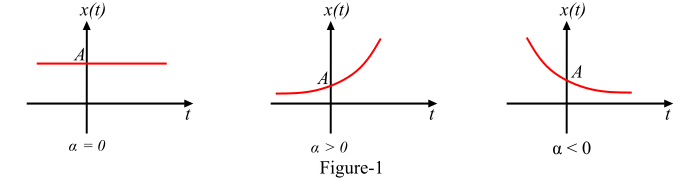
当 𝛼 = 0 时，指数信号 x(t) 在所有时间都是恒定幅度的信号。
当 𝛼 > 0，即 𝛼 为正数时，指数信号 x(t) 是一个增长指数信号。
当 𝛼 < 0，即 𝛼 为负数时，信号 x(t) 是一个衰减指数信号。
这三种信号的波形如图 1 所示。
离散时间实指数信号
在离散时刻定义的实指数信号称为离散时间实指数信号或序列。离散时间实指数序列定义为：
𝑥(𝑛) = 𝑎𝑛 对所有 𝑛
根据 a 的值，离散时间实指数信号可以是以下类型：
当 a < -1 时，指数序列 x(n) 指数增长。
当 0 < a < 1 时，指数信号 x(n) 指数衰减。
当 a < 0 时，指数序列 x(n) 具有交替的符号。
这三种信号在图 2 中以图形方式表示。
复指数信号
样本为复数（即具有实部和虚部）的指数信号称为复指数信号。
连续时间复指数信号
连续时间复指数信号是在每一个时刻都定义的信号。连续时间复信号定义为：
𝑥(𝑡) = 𝐴𝑒𝑠𝑡
其中，
A 是信号的幅度。
s 是一个复变量。
复变量 s 定义为：
𝑠 = 𝜎 + 𝑗𝜔
因此，连续时间复函数也可以写成
𝑥(𝑡) = 𝐴𝑒(𝜎+𝑗𝜔)𝑡 = 𝐴𝑒𝜎𝑡𝑒𝑗𝜔𝑡
⟹ 𝑥(𝑡) = 𝐴𝑒𝜎𝑡(cos 𝜔𝑡 + 𝑗 sin 𝜔𝑡)
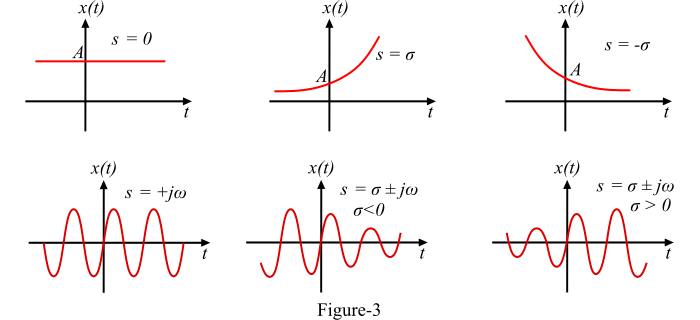
根据 𝜎 和 𝜔 的值，我们得到不同的波形，如图 3 所示。
离散时间复指数序列
在离散时刻定义的复指数信号称为离散时间复指数序列。数学上，离散时间复指数序列定义为：
$$\mathrm{x(n)=a^{n}e^{j(\omega _{0}n+\varphi )}=a^{n}\cos (\omega _{0}n+\varphi)+ja^{n}\sin (\omega _{0}n+\varphi)}$$
根据 a 的大小，我们得到不同类型的离散时间复指数信号：
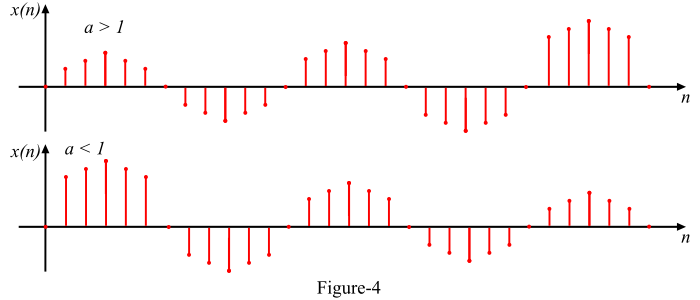
对于 |𝑎| = 1，复指数序列的实部和虚部都是正弦的。
对于 |𝑎| > 1，正弦序列的幅度呈指数增长。
对于 |𝑎| < 1，正弦序列的幅度呈指数衰减。
这些信号的图形表示如图 4 所示。
17K+ 次浏览
