信号与系统：因果信号、非因果信号和反因果信号

因果信号

如果连续时间信号 𝑥(𝑡) 在 𝑡 < 0 时 𝑥(𝑡) = 0，则称该信号为因果信号。因此，因果信号在负时间内不存在。单位阶跃信号 u(t) 是因果信号的一个例子，如图 1 所示。

类似地，如果离散时间序列 x(n) 在 n < 0 时 x(n) = 0，则称该序列为因果序列。

反因果信号

如果连续时间信号 x(t) 在 t > 0 时 x(t) = 0，则称该信号为反因果信号。因此，反因果信号在正时间内不存在。时间反转的单位阶跃信号 u(-t) 是反因果信号的一个例子（参见图 2）。

类似地，如果离散时间序列 x(n) 在 𝑡 > 0 时 x(n) = 0，则称该序列为反因果序列。

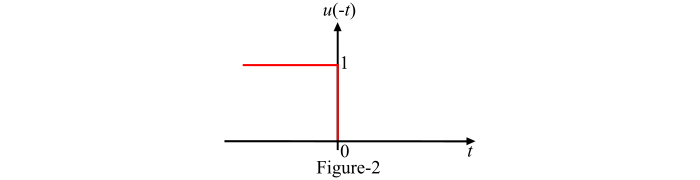
非因果信号

不是因果信号的信号称为非因果信号。因此，根据定义，在正时间和负时间都存在的信号既不是因果信号也不是反因果信号，它是非因果信号。正弦和余弦信号是非因果信号的例子（参见图 3）。

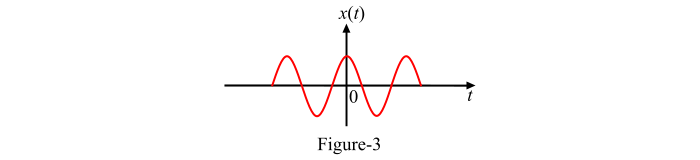
重要 – 所有反因果信号都是非因果信号，但反之则不成立。

数值示例

找出以下哪些信号是因果信号、反因果信号或非因果信号：

• $\mathrm{x(t)=e^{3t}u(t-2)}$

• $\mathrm{x(t)=\sin 5t\: u(t)}$

• $\mathrm{x(t)=4u(-t)}$

• $\mathrm{x(n)=u(-n)}$

• $\mathrm{x(t)=\cos 3t}$

• $\mathrm{x(n)=u(n+3)-u(n-3)}$

解决方案

• 给定的信号是：

  $$\mathrm{x(t)=e^{3t}u(t-2)}$$

  这里，𝑢(𝑡 − 2) 在 t < 0 时为 0，因此，信号 x(t) 在 t < 0 时为 0。因此，给定的信号 x(t) 是因果信号。

• 给定：

  $$\mathrm{x(t)=\sin 5t\: u(t)}$$

  由于单位阶跃信号 u(t) 在负时间内不存在。因此，信号 x(t) 是因果信号，因为 x(t) 在 t < 0 时为 0。

• 给定的信号是：

  $$\mathrm{x(t)=4u(-t)}$$

  给定的信号 x(t) 仅在负时间（即 t < 0）存在。因此，它是反因果信号。它也可以称为非因果信号。

• 给定

  $$\mathrm{x(n)=u(-n)}$$

  给定的信号 x(n) 仅在负时间（即 n < 0）存在。因此，它是反因果的。它也可以称为非因果信号。

• 给定的信号是

  $$\mathrm{x(t)=\cos 3t}$$

  给定的信号 x(t) 是一个余弦信号，其存在范围为 (−∞ 到 ∞)。因此，它是非因果信号。

• 给定

  $$\mathrm{x(n)=u(n+3)-u(n-3)}$$

  给定的信号 x(n) 存在于 𝑛 = −3 到 𝑛 = 3，即信号在正时间和负时间都存在。因此，它是非因果信号。

Manish Kumar Saini

更新于： 2021年11月10日

26K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习