数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学信号与系统 – 信号的时间尺度变换
什么是时间尺度变换？
将一个常数乘以信号的时间轴的过程称为**信号的时间尺度变换**。根据常数或比例因子的值，信号的时间尺度变换可能是时间压缩或时间扩展。信号的时间尺度变换在数据需要以某种速率输入并以不同速率输出时非常有用。
连续时间信号的时间尺度变换
连续时间信号 x(t) 的时间尺度变换可以通过用 'αt' 代替函数中的 't' 来实现。数学上，它表示为：
𝑥(𝑡) → 𝑦(𝑡) = 𝑥(𝛼𝑡)
其中，α 是一个常数，称为比例因子。
如果 α > 1，则信号的时间被压缩 α 倍，信号的时间尺度变换称为时间压缩。而如果 α < 1，则信号的时间被扩展 α 倍，时间尺度变换称为时间扩展。
示例
考虑图 1 所示的连续时间信号 x(t)。可以看出，信号 x(t) 在时间区间 t = (-2) 到 t = 0 时线性地从 0 增加到 5，在时间区间 t = 0 到 t = 3 时保持在 5 不变，然后在时间区间 t = 3 到 t = 5 时线性地从 5 减小到 0。
**情况一** – 考虑信号的时间尺度变换（压缩）：
𝑥(𝑡) → 𝑦(𝑡) = 𝑥(2𝑡)
由于比例因子 α = 2，即 α > 1，因此发生信号的时间压缩，压缩后的信号如图 2 所示。
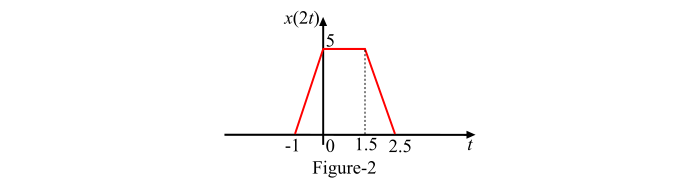
这里可以看出，时间压缩信号 x(2t) 在时间区间 𝑡 = − (2/2) 到 𝑡 = 0 时线性地从 0 增加到 5，在时间区间 t = 0 到 t = (3/2) 时保持在 5 不变，然后在时间区间 t = (3/2) 到 t = (5/2) 时线性地从 5 减小到 0。
**情况二** – 考虑信号的时间尺度变换（扩展）：
$$\mathrm{x(t)\rightarrow y(t)=x\left ( \frac{t}{2} \right )}$$
在这种情况下，α = (1/2)，即 α < 1，因此信号的时间扩展如图 3 所示。
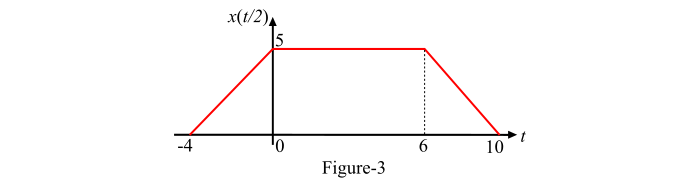
在图 3 中，时间扩展信号 x(t/2) 在时间区间 t = (-2×2) 到 t = 0 时线性地从 0 增加到 5，在时间区间 t = 0 到 t = (3×2) 时保持在 5 不变，然后在时间区间 t = (3×2) 到 t = (5×2) 时线性地从 5 减小到 0。
离散时间序列的时间尺度变换
考虑图 4 所示的离散时间序列 x(n)。
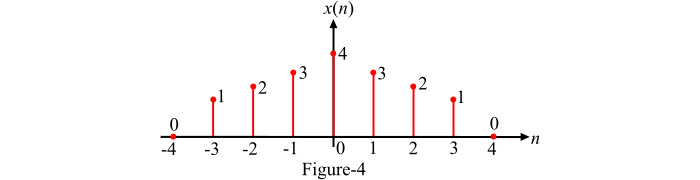
离散序列的时间尺度变换可以定义为：
𝑥(𝑛) → 𝑦(𝑛) = 𝑥(𝑘𝑛)
**情况一** – 如果 k = 2，则
𝑥(𝑛) → 𝑦(𝑛) = 𝑥(2𝑛)
这里，k > 1，因此信号的时间被压缩。我们可以通过代入不同的 n 值来绘制时间压缩信号 y(n)，如图 5 所示。
𝑛 = 0 → 𝑦(0) = 𝑥(0) = 1
𝑛 = (−1) → 𝑦(−1) = 𝑥(−2) = −2
𝑛 = (−2) → 𝑦(−2) = 𝑥(−4) = 0
𝑛 = 1 → 𝑦(1) = 𝑥(2) = 2
𝑛 = 2 → 𝑦(2) = 𝑥(4) = 0
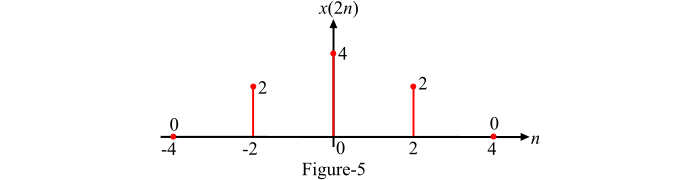
因此，要绘制信号 x(2n)，我们必须跳过信号 x(n) 中的奇数编号样本。
**情况二** – 如果 k = (1/2)，则
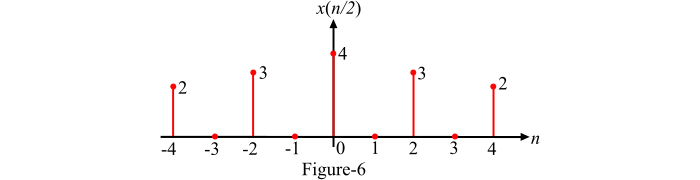
$$\mathrm{x(n)\rightarrow y(n)=x\left ( \frac{n}{2} \right )}$$
由于 k < 1，因此信号被扩展 2 倍。我们可以通过代入不同的 n 值来绘制时间扩展信号 y(n)：
𝑛 = 0 → 𝑦(0) = 𝑥(0) = 1
𝑛 = 2 → 𝑦(2) = 𝑥(1) = 3
𝑛 = 4 → 𝑦(4) = 𝑥(2) = 2
𝑛 = (−2) → 𝑦(−2) = 𝑥(−1) = 3
𝑛 = (−4) → 𝑦(−4) = 𝑥(−2) = 2
在这种情况下，x(n/2) 中的所有奇数分量都为零，因为信号 x(n) 在采样瞬间之间没有任何值。图 6 显示了信号 $\mathrm{y(n)=x\left ( \frac{n}{2} \right )}$ 的图。
浏览量 18K+
