信号与系统：线性时不变系统

---

线性时不变 (LTI) 系统

一个同时具有线性性和时不变性的系统被称为**线性时不变系统**或**LTI系统**。

使用LTI系统有两个主要原因：

• 数学分析变得更容易。

• 许多物理过程虽然不是绝对的LTI系统，但可以用线性和平移不变性的特性来近似。

连续时间LTI系统

LTI系统总是相对于冲激响应来考虑的。这意味着输入是冲激信号，输出是冲激响应。

考虑图1所示的连续时间LTI系统的框图。

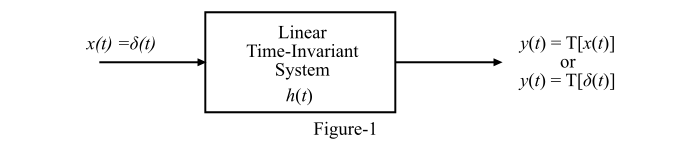
这里，系统的输入是冲激信号，即：

𝑥(𝑡) = 𝛿(𝑡)

系统的冲激响应为

𝑦(𝑡) = ℎ(𝑡) = 𝑇[𝛿(𝑡)]

根据信号的移位特性，任何信号都可以表示为加权和移位的冲激信号的组合，即：

$$\mathrm{x(t)=\int_{-\infty }^{\infty }x(\tau )\delta \left ( t-\tau \right )d\tau}$$

然后，冲激响应为：

$$\mathrm{y(t)=T\left [x(t) \right ]=\int_{-\infty }^{\infty }x(\tau )T\left [ \delta \left ( t-\tau \right ) \right ]d\tau}$$

$$\mathrm{\Rightarrow y(t)=\int_{-\infty }^{\infty }x(\tau )h\left ( t-\tau \right )d\tau\: \:\: ...(1)}$$

公式(1)中的表达式称为**卷积积分**。

卷积积分的符号表示为：

𝑦(𝑡) = 𝑥(𝑡) * ℎ(𝑡)   … (2)

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

离散时间LTI系统

离散时间LTI系统如图2所示。

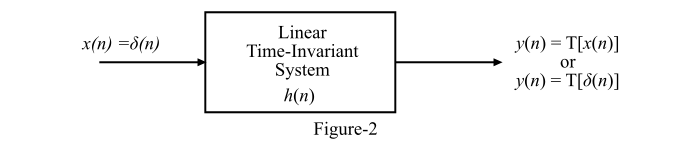
这里，系统的输入是冲激信号，即：

𝑥(𝑛) = 𝛿(𝑛)

系统的离散时间冲激响应为：

𝑦(𝑛) = ℎ(𝑛) = 𝑇[𝛿(𝑛)]

根据信号的移位特性，任何信号都可以表示为加权和移位的冲激信号的组合，即：

$$\mathrm{x(n)=\sum_{k=-\infty }^{\infty }x(k)\, \delta (n-k)}$$

因此，系统的冲激响应为：

$$\mathrm{y(n)=T\left [ \delta (n) \right ]=\sum_{k=-\infty }^{\infty }x(k)\, T\left [ \delta (n-k) \right ]}$$

$$\mathrm{\Rightarrow y(n)=\sum_{k=-\infty }^{\infty }x(k)\,h(n-k)\: \: \cdot \cdot \cdot (3)}$$

公式(3)的表达式称为卷积和。卷积和可以用符号表示为：

𝑦(𝑛) = 𝑥(𝑛) * ℎ(𝑛)   … (4)

此外，

$$\mathrm{ y(n)=\sum_{k=-\infty }^{\infty }x(k)\,h(n-k)=\sum_{k=-\infty }^{\infty }x(n-k)\,h(k)\: \: \cdot \cdot \cdot (5)}$$