数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中二叉树中两个叶子节点之间的最小和路径
问题陈述
给定一棵二叉树，其中每个节点元素都包含一个数字。任务是找到从一个叶子节点到另一个叶子节点的最小可能和。
示例
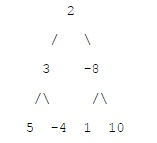
在上面的树中，最小的子路径如下：-6：(-4) + 3 + 2 + (-8) + 1
算法
这个想法是在递归调用中保持两个值：
- 当前节点下的子树从根到叶子的最小路径和
- 叶节点之间的最小路径和
- 对于每个访问过的节点 X，我们必须在 X 的左右子树中找到从根到叶子的最小和。然后将这两个值与 X 的数据相加，并将和与当前最小路径和进行比较
示例
#include <bits/stdc++.h>
using namespace std;
typedef struct node {
int data;
struct node *left;
struct node *right;
} node;
node *newNode(int data) {
node *n = new node;
n->data = data;
n->left = NULL;
n->right = NULL;
return n;
}
int getMinPath(node *root, int &result) {
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return root->data;
}
int leftSum = getMinPath(root->left, result);
int rightSum = getMinPath(root->right, result);
if (root->left && root->right) {
result = min(result, root->data + leftSum + rightSum);
return min(root->data + leftSum, root->data + rightSum);
}
if (root->left == NULL) {
return root->data + rightSum;
} else {
return root->data + leftSum;
}
}
int getMinPath(node *root) {
int result = INT_MAX;
getMinPath(root, result);
return result;
}
node *createTree() {
node *root = newNode(2);
root->left = newNode(3);
root->right = newNode(-8);
root->left->left = newNode(5);
root->left->right = newNode(-4);
root->right->left = newNode(1);
root->right->right = newNode(10);
return root;
}
int main() {
node *root = createTree();
cout << "Minimum sum path = " << getMinPath(root) << endl;
return 0;
}编译并执行上面的程序后，它会生成以下输出：
输出
Minimum sum path = -6
更新于：2019 年 12 月 20 日
167 次浏览
广告