数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究OpenCV Python – 如何查找图像中点到轮廓的最短距离？
我们可以使用 **cv2.pointPolygonTest()** 计算图像中点到轮廓的最短距离，将轮廓点坐标和点坐标作为参数传递。在应用 **cv2.pointPolygonTest()** 之前，我们需要计算图像中的轮廓。我们可以按照以下步骤查找图像中给定点到对象轮廓的最短距离：
导入所需的库。在以下所有 Python 示例中，所需的 Python 库是 **OpenCV**。确保您已安装它。
使用 **cv2.imread()** 读取输入图像。使用此方法读取的 RGB 图像为 BGR 格式。可以选择将读取的 BGR 图像分配给 img。
现在，使用 **cv2.cvtColor()** 函数将此 BGR 图像转换为灰度图像，如下所示。可以选择将转换后的灰度图像分配给 **gray**。
对灰度图像应用阈值处理，将其转换为二值图像。调整第二个参数 (**threshValue**) 以获得更好的二值图像。
查找二值图像中的轮廓。
选择第一个轮廓作为 **cnt** 或循环遍历所有轮廓。
使用 **cv2.pointPolygonTest()** 函数计算点与所选轮廓之间的最短距离。将所需的参数传递给此函数。要计算点 (**250,250**) 和轮廓 **cnt** 之间的最短距离，我们使用以下代码片段
dist = cv2.pointPolygonTest(cnt,(250,250),True)
打印计算出的点与输入图像中对象轮廓之间的最短距离。
在图像中绘制点和检测到的轮廓，以获得更好的可视化效果。
让我们了解如何借助一些 Python 示例查找图像中给定点到对象轮廓的最短距离。
示例
在这个 Python 程序中，我们在输入图像上取了两个点 (250,250) 和 (350,250)。我们计算点与输入图像中轮廓之间的最短距离。输入图像只有一个对象轮廓。我们还在图像上绘制轮廓和点以方便理解。
# import required libraries import cv2 # load the input image img = cv2.imread('four-point-star.png') # convert the input image to grayscale gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # apply thresholding to convert grayscale to binary image ret,thresh = cv2.threshold(gray,150,255,0) # find the contours contours,hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) print("Number of contours detected:", len(contours)) # select the first contour cnt = contours[0] # find the shortest distance from point[250,250] dist1 = cv2.pointPolygonTest(cnt,(250,250),True) # print the shortest distance between the point 1 and contour detected. print('Shortest distance of Point 1 from contour:', dist1) dist2 = cv2.pointPolygonTest(cnt,(350,250),True) # print the shortest distance between the point 2 and contour detected. print('Shortest distance of Point 2 from contour:', dist2) # draw the point [250,250] on the image cv2.circle(img, (250,250), 4, (0, 0, 255), -1) cv2.putText(img, "Point 1", (255,255), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) cv2.circle(img, (350,250), 4, (0, 0, 255), -1) cv2.putText(img, "Point 2", (355,255), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) # draw contour on the input image cv2.drawContours(img, [cnt], -1, (0,255,255), 3) # display the image with drawn extreme points while True: cv2.imshow("Extreme Points", img) if cv2.waitKey(1) & 0xFF == 27: break cv2.destroyAllWindows()
我们将此图像用作此程序的 **输入文件**：
输出
运行上述程序后，将生成以下输出：
Number of contours detected: 1 Shortest distance of Point 1 from contour: -17.72004514666935 Shortest distance of Point 2 from contour: 31.622776601683793
并且我们得到以下窗口，显示了轮廓和两个点：
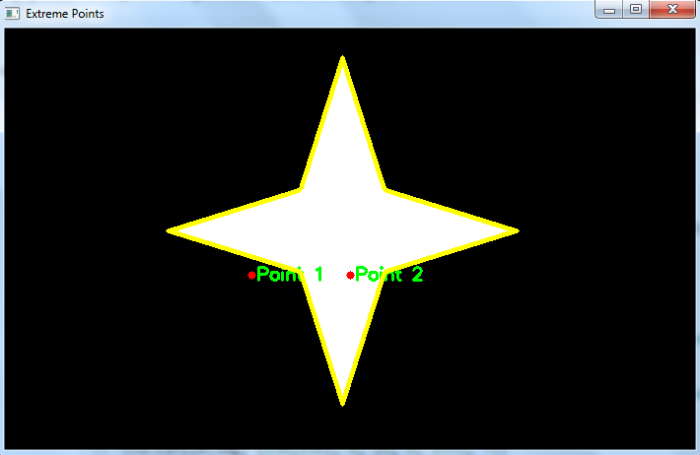
在上面的输出图像中，轮廓以黄色绘制，两个点以红色绘制。点 1 与轮廓之间的最短距离为负数，表明该点位于轮廓外部。点 2 与轮廓之间的最短距离为正数，表明该点位于轮廓内部。如果最短距离为零，则表示该点位于轮廓边界上
示例
在这个 Python 程序中，我们在输入图像上取了一个点 (350,250)。我们检测输入图像中的所有对象轮廓。图像有三个轮廓。我们计算点与输入图像中轮廓之间的最短距离。我们还在图像上绘制轮廓和点以方便理解。
# import required libraries import cv2 # load the input image img = cv2.imread('convexhull.png') # convert the input image to grayscale gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # apply thresholding to convert grayscale to binary image ret,thresh = cv2.threshold(gray,100,255,0) # find the contours contours,hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE) print("Number of contours detected:", len(contours)) # draw contour and shape number for i, cnt in enumerate(contours): M = cv2.moments(cnt) x1, y1 = cnt[0,0] img1 = cv2.drawContours(img, [cnt], -1, (0,255,255), 3) cv2.putText(img, f'Contour:{i+1}', (x1, y1), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2) # compute shortest distance of point (350,250) from the contour dist = cv2.pointPolygonTest(cnt,(350,250),True) print(f'Shortest distance of Point (350,250) from contour {i+1}:', dist) cv2.circle(img, (350,250), 4, (0, 0, 255), -1) cv2.imshow("Shapes", img) cv2.waitKey(0) cv2.destroyAllWindows()
我们将此图像用作此程序的 **输入文件**：
输出
运行上述程序后，将生成以下输出：
Number of contours detected: 3 Shortest distance of Point (350,250) from contour 1: -83.73768566183328 Shortest distance of Point (350,250) from contour 2: -62.81719509815764 Shortest distance of Point (350,250) from contour 3: -57.27564927611035
并且我们得到以下窗口，显示了轮廓和点：
在上面的输出图像中，轮廓以黄色绘制，点以红色绘制。点与轮廓之间的每个最短距离都为负数，表明该点位于每个轮廓的外部。与其他距离相比，点与轮廓 3 之间的绝对距离最小。因此，该点最靠近轮廓 3。
4K+ 浏览量
