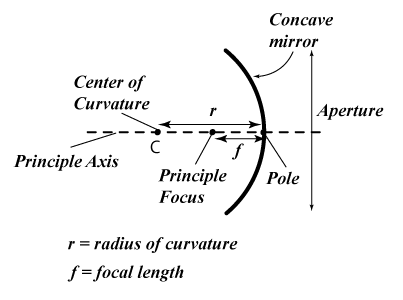
定义以下术语？1.极 2.主轴 3.焦点 4.曲率中心
1) 极：镜子的球面表面的中心，称为镜子的极。
2) 主轴: 通过极 P 和镜子的曲率中心 C 的直线，称为主轴。
3) 焦点:它是镜子的主轴上的一个点，使得入射到镜子上平行于主轴的光线在反射后，在凹面镜的情况下，实际上会聚于此点，或在凸面镜的情况下，看起来像是从该点发出。
4) 曲率中心: 镜面构成一部分的球壳的中心，称为镜子的曲率中心。它位于表面之外。
- 相关文章
- 关于球面镜，定义以下术语：（i）极（ii）曲率中心（iii）主轴（iv）主焦点
- 定义凹面镜的主焦点。
- 曲率半径和主轴的区别。
- 凹面镜产生+4的放大倍率。物体放置在：（a）焦点处（b）焦点和曲率中心之间（c）焦点和极之间（d）曲率中心以外
- 定义球面镜的主轴。
- 观察到凹面镜形成的像是虚像、正立且大于物体。物体的位置应该在哪里？$(a)$. 焦点和曲率中心之间$(b)$. 曲率中心处$(c)$. 曲率中心以外$(d)$. 镜子的极和其主焦点之间。
- （a）定义（i）凹面镜的主焦点，以及（ii）凹面镜的焦距。（b）画图表示凹面镜对一束平行光线的反射作用。在此图上标记凹面镜的主轴、焦点 F、曲率中心 C、极 P 和焦距 f。
- 观察以下模式$1=\frac{1}{2}\{1 \times(1+1)\}$$1+2=\frac{1}{2}\{2 \times(2+1)\}$$1+2+3=\frac{1}{2}\{3 \times(3+1)\}$$1+2+3+4=\frac{1}{2}\{4 \times(4+1)\}$并求出以下每个值：（i）$1 + 2 + 3 + 4 + 5 +….. + 50$(ii)$31 + 32 +… + 50$
- 为了用凹面镜获得-2（负2）的放大倍率，物体应该放置在：（a）极和焦点之间（b）焦点和曲率中心之间（c）曲率中心处（d）曲率中心以外
- 如果入射光线通过焦点，则反射光线将（a）通过极（b）平行于主轴（c）原路返回（d）通过曲率中心
- 用 C++ 计算级数 1 + (1+2) + (1+2+3) + (1+2+3+4) + ... + (1+2+3+4+...+n) 的和
- 化简以下每个式子：$\frac{1}{3}$ of $1 \frac{1}{4}+2 \frac{1}{3}$
- 求以下各数的比值：$2 \frac{1}{2}$ 比 $4$ 比 $3 \frac{1}{3}$
- 以下数据给出 41 个家庭中孩子的数量：$1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.$将其表示为频数分布的形式。
- 化简以下式子：$3^0 + (-4)^{-1} \times 2^2$.
开启你的 职业生涯
通过完成课程获得认证
开始学习
数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
