数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中二维打印二叉树
在这个问题中，我们给定一棵二叉树，需要将其打印到二维平面上。
二叉树是一种特殊的树，其每个节点最多有两个子节点。因此，每个节点要么是叶子节点，要么有一个或两个子节点。
示例：
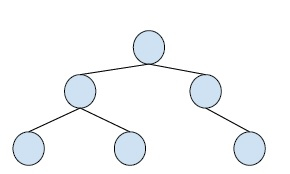
让我们举一个例子来更好地理解这个主题：
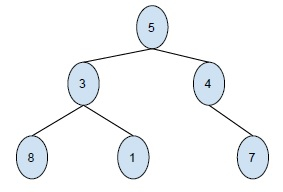
输出 -
7 4 5 1 3 8
正如我们在示例中看到的，树的节点以水平方式打印到二维输出屏幕上。
在这里，我们将树旋转了 90 度。
让我们看看新的水平树由什么组成：
树的数据结构以水平方式存储，包括
根节点位于水平视图中第一个位置，起始行下方 n 行。即根节点将位于第 n 行的开头。
树的新层位于 n+i 行和 n-i 行。并且距离行首 i 个制表符空格。
树的最右边的叶子节点打印在第一行。而树的最左边的节点打印在最后一行。
示例
让我们根据此逻辑创建一个程序：
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
#define COUNT 10
class Node{
public:
int data;
Node* left, *right;
Node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
void printTree(Node *root, int space){
if (root == NULL)
return;
space += COUNT;
printTree(root->right, space);
for (int i = COUNT; i < space; i++)
cout<<"\t";
cout<<root->data<<"\n";
printTree(root->left, space);
}
int main(){
Node *root = new Node(43);
root->left = new Node(25);
root->right = new Node(67);
root->left->left = new Node(14);
root->left->right = new Node(51);
root->right->left = new Node(26);
root->right->right = new Node(97);
root->left->left->left = new Node(81);
root->left->left->right = new Node(49);
root->left->right->left = new Node(07);
root->left->right->right = new Node(31);
root->right->left->left = new Node(29);
root->right->left->right = new Node(13);
root->right->right->left = new Node(59);
root->right->right->right = new Node(16);
printTree(root, 0);
return 0;
}输出
16 97 59 67 13 26 29 43 31 51 7 25 49 14 81
更新于：2020-01-03
899 次查看
广告