Python程序：检查选择矩阵空单元格的方案数

假设我们有一个 N x N 的二进制矩阵，其中 0 表示空单元格，1 表示被阻塞的单元格，我们需要找到选择 N 个空单元格的方案数，使得每一行和每一列至少包含一个选中的单元格。如果答案非常大，则返回结果模 10^9 + 7。

因此，如果输入如下所示：

那么输出将为 4，因为我们有以下配置（其中 x 是选中的单元格）：−

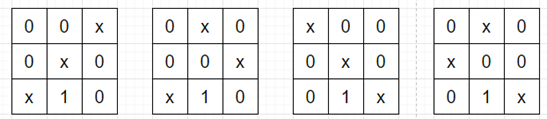
为了解决这个问题，我们将遵循以下步骤：−

• n := 矩阵的大小
• 定义一个函数 f()。它将接收 i 和 bs 作为参数。
• 如果 i >= n，则
  • 返回 1
• ans := 0
• 对于 j 从 0 到 n，执行以下操作：
  • 如果 matrix[i, j] 等于 0 且 (2^j AND bs 等于 0)，则
    • ans := ans + f(i + 1, bs OR 2^j)
• 返回 ans
• 从主方法调用并返回 f(0, 0)

让我们看看下面的实现，以便更好地理解：−

示例

在线演示

class Solution:
   def solve(self, matrix):
      n = len(matrix)

      def f(i, bs):
         if i >= n:
            return 1
         ans = 0
         for j in range(n):
            if matrix[i][j] == 0 and ((1 << j) & bs == 0):
               ans += f(i + 1, bs | (1 << j))
         return ans

      return f(0, 0)

ob = Solution()
matrix = [
   [0, 0, 0],
   [0, 0, 0],
   [0, 1, 0]
]
print(ob.solve(matrix))

输入

[  
[0, 0, 0],  
[0, 0, 0],  
[0, 1, 0] ]

输出

4

Arnab Chakraborty

更新于： 2020-12-03

浏览量 155 次

开启您的 职业生涯

完成课程获得认证

开始学习