数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究Python程序：找出公民能够到达市场的最小成本
假设有n个城市和m条连接这些城市的道路。市民需要市场来购买商品。现在，城市里没有市场，城市之间的道路正在建设中。如果满足以下条件，则可以在两个城市之间修建双向道路：(i) 该城市包含一个市场；(ii) 可以通过连接有市场的道路到达这些城市。修建道路的成本为x，修建市场的成本为y，两者均已给出。我们需要找出使每个城市的市民都能到达市场的最小成本。数组'cities'包含有关城市的信息，说明哪些城市可以通过道路连接。
因此，如果输入类似于n = 4，m = 3，x = 1，y = 2，cities = [[1, 2], [2, 3], [3, 4]]，则输出将为4。
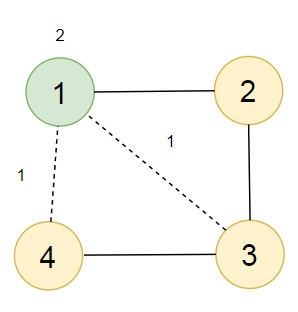
在这里，我们可以看到四个城市1、2、3和4。如果在城市1处建立一个市场，并在(1, 4)和(1,3)之间修建两条道路，则总成本将为2 + 1 + 1 = 4。这是最小成本。
为了解决这个问题，我们将遵循以下步骤：
- 如果x <= y，则
- 返回n * x
- 否则，
- adj_list := 一个包含列表作为元素的映射
- 对于cities中的每个城市，执行以下操作：
- city1 := city[0]
- city2 := city[1]
- 将city2插入adj_list[city1]的末尾
- 将city1插入adj_list[city2]的末尾
- temp := 一个大小为(n + 1)的新列表，初始化值为True
- value := 0
- dq := 一个双端队列
- 对于cur从1到n + 1，执行以下操作：
- 如果temp[cur]不为零，则
- value := value + x
- 将cur插入dq的最右边
- temp[cur] := False
- 当dq不为空时，执行以下操作：
- 对于dq中提取的左侧元素的每个相邻元素i，执行以下操作：
- 如果temp[i]不为零，则
- 将i插入dq的最右边
- temp[i] := False
- value := value + y
- 如果temp[i]不为零，则
- 如果temp[cur]不为零，则
- 返回value
示例
让我们看看以下实现以更好地理解：
from collections import defaultdict, deque
def solve(n, m, x, y, cities):
if x <= y:
return n * x
else:
adj_list = defaultdict(list)
for city in cities:
city1 = city[0]
city2 = city[1]
adj_list[city1].append(city2)
adj_list[city2].append(city1)
temp = [True] * (n + 1)
value = 0
dq = deque()
for cur in range(1, n + 1):
if temp[cur]:
value += x
dq.append(cur)
temp[cur] = False
while dq:
for i in adj_list[dq.popleft()]:
if temp[i]:
dq.append(i)
temp[i] = False
value += y
return value
print(solve(4, 3, 1, 2, [[1, 2], [2, 3], [3, 4]]))输入
4, 3, 2, 1, [[1, 2], [2, 3], [3, 4]]
输出
4
更新于： 2021年10月23日
264 次查看
广告