C++程序：求直线的斜率

在本文中，我们将学习如何使用程序找到直线的斜率。但在进入程序之前，让我们首先了解直线的斜率在数学中代表什么，以及如何在 C++ 中使用其数学公式来计算它。

在数学中，直线的斜率是一个数值，用于衡量直线的倾斜度和方向。它表示当您沿直线从左到右（或水平）移动时，直线上升或下降的速率。通常用字母“m”表示。在数学中，倾斜度指的是直线的斜率或梯度。

从数学角度来说，它代表直线上任意两点之间垂直方向（y 轴）的变化量与水平方向（x 轴）的变化量的比值。这个比值可以表示为m = y 的变化量 / x 的变化量。

要找到直线的斜率，您必须知道直线上的两个点。假设这两个点是 (x1, y1) 和 (x2, y2)。然后，斜率 m 计算如下：

Slope (m) = (Y2 - Y1)/(X2 - X1)

让我们通过输入和输出场景来了解输入值如何与所需的输出相关联：

输入

p1(-1, 1),  p2(3, 3)

输出

0.5

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

说明

使用斜率 (m) 公式 =(Y2 - Y1)/(X2 - X1)，假设值为

x1 = -1, y1 = 1
x2 = 3,  y2 = 3
The slope of line = 1/2 = 0.5

下图中，我们绘制了一条直线的斜率，并标出了两个点，分别为 (x1, y1) 和 (x2, y2) 轴值。程序中将使用相同的点值来求直线的斜率：

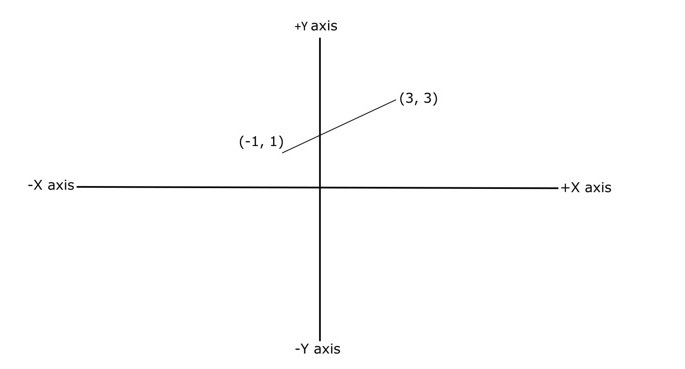
以下是查找直线斜率的分步过程：

确定直线上具有值的两个坐标。为了简化此表达式，我们可以将它们称为 (x1, y1) 和 (x2, y2)。

通过减去两个点的 y 坐标来计算垂直方向的变化量 (Δy)。

Δ𝑦=y2−y1.

通过减去两个点的 x 坐标来计算水平方向的变化量 (Δ𝑥)。

Δx=x2−x1.

为了找到直线的斜率，我们将使用定义的几何公式，使用位于直线上的任意两点 p1(x1, y1) 和 p2(x2, y2) 来求直线的斜率。

Slope (m) = Δy/Δx = y2−y1/ x2−x1 (Here Δ𝑥 and Δ𝑦 means change in movement.)

示例

以下是使用 C++ 查找直线斜率的程序：

Open Compiler
#include <iostream>
#include <iomanip> 
using namespace std;
float calcSlope(float point[2][2]){
   float slope = ((point[1][1] - point[0][1]) / (point[1][0] - point[0][0]));
   return slope;
}
int main() {
   float points[2][2] = {{-1, 1}, {3, 3}};
   cout << "The slope of the line is " << fixed << setprecision(2) << calcSlope(points) << endl;
   return 0;
}

输出

The slope of the line is 0.50

以下是一些关于直线斜率的关键点：

  • 根据直线如何倾斜向上、倾斜向下或没有形状，斜率可以是正数、负数、零或未定义。
  • 如果斜率为正，则直线将从左到右向上倾斜。从左到右移动将是一系列的增加。
  • 如果斜率仍然为零，则直线是水平的。但是，此斜率也可能导致未定义的斜率，这意味着直线是垂直的。

更新于： 2024-05-22

1K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告