Python深度学习 - 快速指南

---

---

Python深度学习 - 简介

深度结构化学习或分层学习，简称深度学习，是机器学习方法家族的一部分，而机器学习本身又是人工智能更广泛领域的一个子集。

深度学习是一类机器学习算法，它使用多层非线性处理单元进行特征提取和转换。每一层都使用前一层输出作为输入。

深度神经网络、深度信念网络和循环神经网络已被应用于计算机视觉、语音识别、自然语言处理、音频识别、社交网络过滤、机器翻译和生物信息学等领域，其产生的结果与人类专家相当，在某些情况下甚至优于人类专家。

深度学习算法和网络 -

• 基于对数据多级特征或表示的无监督学习。高级特征源自低级特征，形成分层表示。

• 使用某种形式的梯度下降进行训练。

Python深度学习 - 环境

在本章中，我们将学习Python深度学习的环境设置。为了构建深度学习算法，我们必须安装以下软件。

• Python 2.7+
• 带有Numpy的Scipy
• Matplotlib
• Theano
• Keras
• TensorFlow

强烈建议通过Anaconda发行版安装Python、NumPy、SciPy和Matplotlib。它包含所有这些软件包。

我们需要确保不同类型的软件正确安装。

让我们转到命令行程序并输入以下命令 -

$ python
Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34)
[GCC 7.2.0] on linux

接下来，我们可以导入所需的库并打印其版本 -

import numpy
print numpy.__version__

输出

1.14.2

Theano、TensorFlow和Keras的安装

在我们开始安装Theano、TensorFlow和Keras软件包之前，我们需要确认是否安装了pip。Anaconda中的包管理系统称为pip。

要确认pip的安装，请在命令行中键入以下内容 -

$ pip

确认pip安装后，我们可以通过执行以下命令来安装TensorFlow和Keras -

$pip install theano
$pip install tensorflow
$pip install keras

通过执行以下代码行确认Theano的安装 -

$python –c “import theano: print (theano.__version__)”

输出

1.0.1

通过执行以下代码行确认Tensorflow的安装 -

$python –c “import tensorflow: print tensorflow.__version__”

输出

1.7.0

通过执行以下代码行确认Keras的安装 -

$python –c “import keras: print keras.__version__”
Using TensorFlow backend

输出

2.1.5

Python深度学习基础机器学习

人工智能（AI）是任何使计算机能够模仿人类认知行为或智能的代码、算法或技术。机器学习（ML）是AI的一个子集，它使用统计方法使机器能够从经验中学习和改进。深度学习是机器学习的一个子集，它使多层神经网络的计算成为可能。机器学习被视为浅层学习，而深度学习被视为具有抽象性的分层学习。

机器学习涉及广泛的概念。这些概念如下所示 -

• 监督学习
• 无监督学习
• 强化学习
• 线性回归
• 成本函数
• 过拟合
• 欠拟合
• 超参数等。

在监督学习中，我们学习从标记数据中预测值。一种有助于此的ML技术是分类，其中目标值是离散值；例如，猫和狗。机器学习中另一种可能提供帮助的技术是回归。回归作用于目标值。目标值是连续值；例如，可以使用回归分析股票市场数据。

在无监督学习中，我们从未标记或未结构化的输入数据中进行推断。如果我们有一百万份医疗记录，我们必须理解它，找到底层结构、异常值或检测异常，我们使用聚类技术将数据划分为广泛的集群。

数据集被划分为训练集、测试集、验证集等。

2012年的一项突破使深度学习的概念变得突出。一种算法使用2个GPU和大型数据等最新技术成功地将100万张图像分类为1000个类别。

深度学习与传统机器学习的关系

传统机器学习模型遇到的主要挑战之一是称为特征提取的过程。程序员需要具体说明并告诉计算机要查找的特征。这些特征将有助于做出决策。

将原始数据输入算法很少有效，因此特征提取是传统机器学习工作流程的关键部分。

这给程序员带来了巨大的责任，并且算法的效率在很大程度上取决于程序员的创造力。对于诸如对象识别或手写识别之类的复杂问题，这是一个巨大的问题。

深度学习能够学习多层表示，是为数不多的帮助我们进行自动特征提取的方法之一。可以假设较低层执行自动特征提取，程序员几乎不需要或不需要任何指导。

人工神经网络

人工神经网络，简称神经网络，并不是一个新概念。它已经存在了大约80年。

直到2011年，随着新技术的应用、海量数据集的可用性和功能强大的计算机，深度神经网络才变得流行起来。

神经网络模仿神经元，神经元具有树突、细胞核、轴突和轴突末梢。

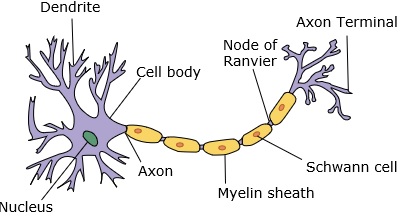
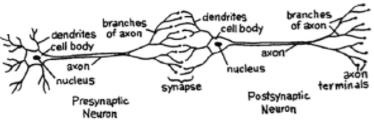
对于一个网络，我们需要两个神经元。这些神经元通过一个神经元树突和另一个神经元轴突末梢之间的突触传递信息。

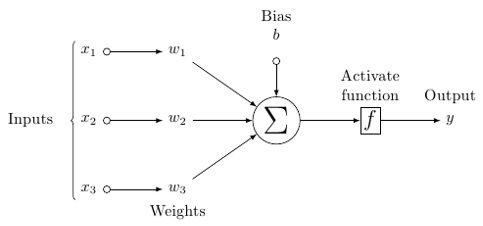
人工神经元的可能模型如下所示 -

神经网络看起来如下所示 -

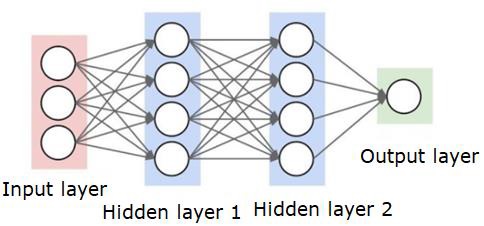
圆圈是神经元或节点，它们对数据执行函数，连接它们的线/边是权重/正在传递的信息。

每一列都是一层。数据的第一层是输入层。然后，输入层和输出层之间的所有层都是隐藏层。

如果你有一个或几个隐藏层，那么你有一个浅层神经网络。如果你有很多隐藏层，那么你有一个深度神经网络。

在这个模型中，你有输入数据，你对其进行加权，并将其通过神经元中的称为阈值函数或激活函数的函数传递。

基本上，它是将所有值与某个值进行比较后的总和。如果你发出信号，则结果为（1）输出，或者没有发出任何信号，则为（0）。然后对其进行加权并传递到下一个神经元，并运行相同类型的函数。

我们可以使用S形（S形）函数作为激活函数。

至于权重，它们最初是随机的，并且每个输入到节点/神经元的权重都是唯一的。

在典型的前馈神经网络（最基本类型的神经网络）中，您让信息直接通过您创建的网络，然后使用样本数据将输出与您希望的输出进行比较。

从这里，你需要调整权重以帮助你的输出与你期望的输出相匹配。

将数据直接发送通过神经网络的过程称为前馈神经网络。

我们的数据按顺序从输入到各层，然后到输出。

当我们向后移动并开始调整权重以最小化损失/成本时，这称为反向传播。

这是一个优化问题。在实际的神经网络中，我们必须处理数十万个变量，甚至数百万个或更多。

第一个解决方案是使用随机梯度下降作为优化方法。现在，有AdaGrad、Adam优化器等选项。无论哪种方式，这都是一个巨大的计算操作。这就是为什么神经网络在半个多世纪以来基本上被束之高阁。直到最近，我们才拥有机器中能够考虑执行这些操作的强大功能和架构，以及与之匹配的适当大小的数据集。

对于简单的分类任务，神经网络的性能与其他简单的算法（如K最近邻）相对接近。当我们拥有更多数据和更复杂的问题时，神经网络的真正效用就会显现出来，这两种情况都优于其他机器学习模型。

深度神经网络

深度神经网络（DNN）是输入层和输出层之间有多个隐藏层的人工神经网络。与浅层人工神经网络类似，DNN可以模拟复杂的非线性关系。

神经网络的主要目的是接收一组输入，对其进行逐步复杂的计算，并输出结果来解决现实世界的问题，例如分类。我们限制自己使用前馈神经网络。

在深度网络中，我们有输入、输出和顺序数据的流。

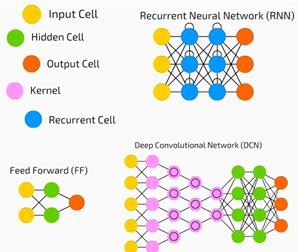
神经网络广泛用于监督学习和强化学习问题。这些网络基于一组相互连接的层。

在深度学习中，隐藏层的数量（主要是非线性的）可能很大；例如大约1000层。

DL模型产生的结果比普通ML网络好得多。

我们主要使用梯度下降方法来优化网络并最小化损失函数。

我们可以使用ImageNet（一个包含数百万张数字图像的存储库）将数据集分类为猫和狗等类别。除了静态图像外，DL网络越来越多地用于动态图像以及时间序列和文本分析。

训练数据集是深度学习模型的重要组成部分。此外，反向传播是训练深度学习模型的主要算法。

深度学习处理具有复杂输入输出转换的大型神经网络的训练。

深度学习的一个例子是将照片映射到照片中人物的姓名，就像他们在社交网络上做的那样，用短语描述图片是深度学习的另一个最新应用。

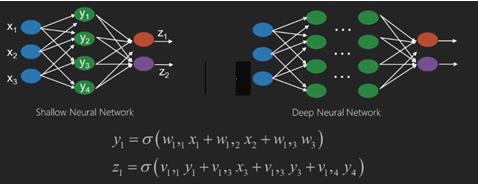
神经网络是具有输入（如x1、x2、x3…）的函数，这些输入被转换为输出（如z1、z2、z3等），在两个（浅层网络）或多个中间操作中，也称为层（深层网络）。

权重和偏差在层与层之间发生变化。“w”和“v”是神经网络各层中的权重或突触。

深度学习的最佳用例是监督学习问题。在这里，我们有一大组数据输入和一组所需的输出。

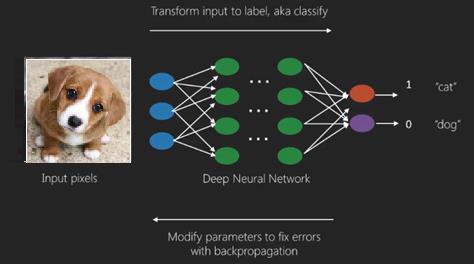
在这里，我们应用反向传播算法来获得正确的输出预测。

深度学习最基本的数据集是MNIST，一个手写数字数据集。

我们可以使用Keras训练一个深度卷积神经网络，以对来自该数据集的手写数字图像进行分类。

神经网络分类器的激发或激活会产生一个分数。例如，要将患者分类为患病和健康，我们考虑身高、体重和体温、血压等参数。

高分表示患者患病，低分表示患者健康。

输出层和隐藏层中的每个节点都有自己的分类器。输入层接收输入并将分数传递到下一个隐藏层以进行进一步激活，依此类推，直到达到输出。

从输入到输出从左到右的这个向前过程称为**前向传播**。

神经网络中的信用分配路径（CAP）是从输入到输出的一系列转换。CAP阐明了输入和输出之间可能存在的因果关系。

给定前馈神经网络的CAP深度或CAP深度是隐藏层的数量加上1，因为输出层包括在内。对于循环神经网络，信号可能多次通过一层，CAP深度可能无限大。

深层网络和浅层网络

没有明确的深度阈值将浅层学习与深度学习区分开来；但大多数人认为，对于具有多个非线性层的深度学习，CAP必须大于2。

神经网络中的基本节点是一个感知器，模仿生物神经网络中的神经元。然后我们有多层感知器或MLP。每组输入都由一组权重和偏差进行修改；每条边都有唯一的权重，每个节点都有唯一的偏差。

神经网络的预测**准确性**取决于其**权重和偏差**。

提高神经网络准确性的过程称为**训练**。前向传播网络的输出与已知正确的输出值进行比较。

**成本函数或损失函数**是生成输出与实际输出之间的差异。

训练的目的是使数百万个训练样本的训练成本尽可能小。为此，网络会调整权重和偏差，直到预测与正确的输出相匹配。

经过良好训练后，神经网络每次都有可能做出准确的预测。

当模式变得复杂并且您希望计算机识别它们时，您必须使用神经网络。在如此复杂的模式场景中，神经网络优于所有其他竞争算法。

现在有GPU可以比以往更快地训练它们。深度神经网络已经在彻底改变人工智能领域。

计算机已被证明擅长执行重复计算和遵循详细的指令，但在识别复杂模式方面却不太擅长。

如果存在识别简单模式的问题，支持向量机（SVM）或逻辑回归分类器可以很好地完成这项工作，但是随着模式复杂性的增加，别无选择，只能转向深度神经网络。

因此，对于像人脸这样复杂的模式，浅层神经网络会失败，别无选择，只能转向具有更多层的深度神经网络。深度网络能够通过将复杂模式分解成更简单的模式来完成其工作。例如，人脸；深度网络将使用边缘来检测嘴唇、鼻子、眼睛、耳朵等部位，然后将它们重新组合以形成人脸。

正确预测的准确性已变得如此精确，以至于最近在谷歌模式识别挑战赛中，深度网络击败了人类。

这种分层感知器网络的想法已经存在一段时间了；在这个领域，深度网络模仿人脑。但其缺点之一是训练时间很长，这是一个硬件限制。

然而，最近的高性能GPU能够在一周内训练出此类深度网络；而快速的CPU可能需要数周甚至数月才能完成相同的工作。

选择深度网络

如何选择深度网络？我们必须确定我们是构建分类器，还是试图在数据中查找模式，以及是否将使用无监督学习。为了从一组未标记的数据中提取模式，我们使用受限玻尔兹曼机或自动编码器。

在选择深度网络时，请考虑以下几点 -

• 对于文本处理、情感分析、解析和命名实体识别，我们使用循环网络或递归神经张量网络或RNTN；

• 对于在字符级别运行的任何语言模型，我们使用循环网络。

• 对于图像识别，我们使用深度信念网络DBN或卷积网络。

• 对于物体识别，我们使用RNTN或卷积网络。

• 对于语音识别，我们使用循环网络。

通常，深度信念网络和具有整流线性单元或RELU的多层感知器都是分类的良好选择。

对于时间序列分析，始终建议使用循环网络。

神经网络已经存在了50多年；但直到现在它们才开始崭露头角。原因是它们很难训练；当我们尝试使用一种称为反向传播的方法训练它们时，我们会遇到一个称为消失或爆炸梯度的问题。发生这种情况时，训练需要更长的时间，准确性会受到影响。在训练数据集时，我们不断计算成本函数，它是预测输出与一组标记训练数据中的实际输出之间的差异。然后通过调整权重和偏差值来最小化成本函数，直到获得最低值。训练过程使用梯度，它是成本相对于权重或偏差值变化的变化率。

受限玻尔兹曼机或自动编码器 - RBM

2006年，在解决消失梯度问题方面取得了突破。Geoffrey Hinton设计了一种新颖的策略，导致了**受限玻尔兹曼机 - RBM**的开发，这是一种浅层两层网络。

第一层是**可见**层，第二层是**隐藏**层。可见层中的每个节点都连接到隐藏层中的每个节点。该网络被称为受限的，因为不允许同一层内的两层共享连接。

自动编码器是将输入数据编码为向量的网络。它们创建原始数据的隐藏或压缩表示。这些向量可用于降维；该向量将原始数据压缩成较少的基本维度。自动编码器与解码器配对，允许根据其隐藏表示重建输入数据。

RBM是双向翻译器的数学等价物。前向传递接收输入并将它们转换为一组编码输入的数字。同时，反向传递接收这组数字并将它们转换回重建的输入。经过良好训练的网络以高精度执行反向传播。

在这两个步骤中，权重和偏差都起着关键作用；它们帮助RBM解码输入之间的相互关系，并决定哪些输入对于检测模式至关重要。通过前向和反向传递，RBM经过训练以使用不同的权重和偏差来重建输入，直到输入和重建尽可能接近。RBM的一个有趣的方面是数据不需要标记。这对于照片、视频、语音和传感器数据等现实世界的数据集非常重要，所有这些数据集往往都是未标记的。RBM无需人工标记数据，即可自动对数据进行排序；通过正确调整权重和偏差，RBM能够提取重要特征并重建输入。RBM是特征提取神经网络家族的一部分，这些网络旨在识别数据中固有的模式。这些也称为自动编码器，因为它们必须编码自己的结构。

深度信念网络 - DBN

深度信念网络（DBN）是通过组合RBM并引入一种巧妙的训练方法形成的。我们有一个新模型，最终解决了消失梯度问题。Geoffrey Hinton发明了RBM和深度信念网络作为反向传播的替代方案。

DBN在结构上类似于MLP（多层感知器），但在训练方面却大不相同。正是训练使DBN能够胜过其浅层对应物。

DBN可以可视化为RBM的堆栈，其中一个RBM的隐藏层是其上方RBM的可见层。第一个RBM经过训练以尽可能准确地重建其输入。

第一个RBM的隐藏层作为第二个RBM的可见层，并且第二个RBM使用第一个RBM的输出进行训练。此过程迭代，直到网络中的每一层都经过训练。

在DBN中，每个RBM都学习整个输入。DBN通过依次微调整个输入来全局工作，因为模型像相机镜头缓慢聚焦图像一样缓慢改进。RBM的堆栈优于单个RBM，就像多层感知器MLP优于单个感知器一样。

在这个阶段，受限玻尔兹曼机（RBM）已经检测到数据中的内在模式，但没有任何名称或标签。为了完成深度信念网络（DBN）的训练，我们必须为这些模式引入标签，并使用监督学习对网络进行微调。

我们需要一个非常小的带标签样本集，以便将特征和模式与名称关联起来。这套带有标签的小数据集用于训练。与原始数据集相比，这套带标签的数据集可以非常小。

权重和偏差会发生微小的变化，导致网络对模式的感知发生细微变化，并且通常会导致整体准确率略有提高。

通过使用GPU，训练可以在合理的时间内完成，并且与浅层网络相比，可以获得非常准确的结果，我们也看到了解决梯度消失问题的方案。

生成对抗网络 - GANs

生成对抗网络是深度神经网络，包含两个相互对抗的网络，因此得名“对抗”。

GANs 于 2014 年由蒙特利尔大学的研究人员发表的一篇论文中提出。Facebook 的人工智能专家 Yann LeCun 在谈到 GANs 时，称对抗训练是“过去 10 年机器学习中最有趣的想法”。

GANs 的潜力巨大，因为网络可以学习模仿任何数据分布。GANs 可以被训练来创建与我们自身世界惊人相似的平行世界，无论是在图像、音乐、语音还是散文领域。从某种意义上说，它们是机器人艺术家，并且它们的输出令人印象深刻。

在 GAN 中，一个神经网络被称为生成器，它生成新的数据实例，而另一个神经网络被称为鉴别器，它评估这些实例的真实性。

假设我们正在尝试生成手写数字，例如 MNIST 数据集中发现的那些数字，这些数字来自现实世界。当鉴别器看到来自真实 MNIST 数据集的实例时，它的工作就是将其识别为真实的。

现在考虑 GAN 的以下步骤 -

• 生成器网络以随机数的形式接收输入，并返回一个图像。

• 生成的图像与来自实际数据集的一系列图像一起作为输入提供给鉴别器网络。

• 鉴别器接收真实和伪造的图像，并返回概率（0 到 1 之间的数字），其中 1 表示预测为真实，0 表示预测为伪造。

• 所以你有一个双重反馈回路 -

  • 鉴别器与我们已知的图像的真实情况处于反馈回路中。

  • 生成器与鉴别器处于反馈回路中。

循环神经网络 - RNNs

RNN是神经网络，其中数据可以沿任何方向流动。这些网络用于语言建模或自然语言处理 (NLP) 等应用。

RNNs 的基本概念是利用顺序信息。在普通的神经网络中，假设所有输入和输出彼此独立。如果我们想预测句子中的下一个单词，我们必须知道它前面的单词。

RNNs 被称为循环神经网络，因为它们对序列的每个元素重复相同的任务，输出基于之前的计算。因此，可以认为 RNNs 具有“记忆”，它捕获有关先前计算的信息。理论上，RNNs 可以使用非常长序列中的信息，但在现实中，它们只能回溯几个步骤。

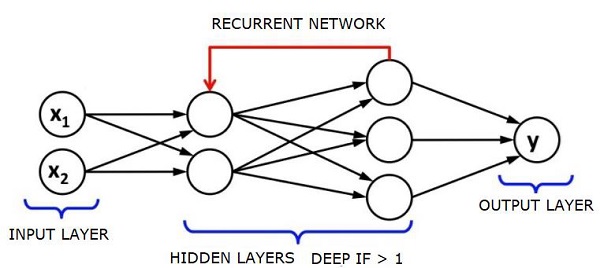
长短期记忆网络 (LSTMs) 是最常用的 RNNs。

与卷积神经网络一起，RNNs 已被用作模型的一部分，用于生成未标记图像的描述。这种方法的效果令人惊叹。

卷积深度神经网络 - CNNs

如果我们增加神经网络的层数以使其更深，则会增加网络的复杂性，并允许我们对更复杂的函数进行建模。但是，权重和偏差的数量将呈指数级增长。事实上，对于普通神经网络来说，学习此类难题可能变得不可能。这导致了一种解决方案：卷积神经网络。

CNNs 广泛应用于计算机视觉；也已应用于声学建模以进行自动语音识别。

卷积神经网络背后的思想是“移动滤波器”的概念，它穿过图像。这个移动滤波器或卷积应用于节点的某个邻域，例如像素，其中应用的滤波器为节点值的 0.5 倍 -

著名研究员 Yann LeCun 开创了卷积神经网络。Facebook 的人脸识别软件使用了这些网络。CNN 已经成为机器视觉项目的首选解决方案。卷积网络有多个层。在 2015 年的 ImageNet 挑战赛中，一台机器在物体识别方面击败了人类。

简而言之，卷积神经网络 (CNNs) 是多层神经网络。层数有时多达 17 层或更多，并假设输入数据为图像。

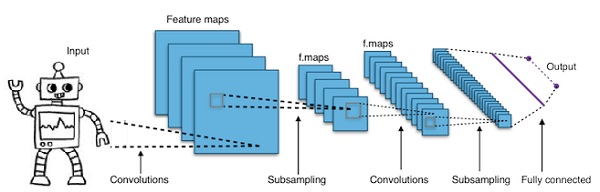
CNNs 大幅减少了需要调整的参数数量。因此，CNNs 可以有效地处理原始图像的高维度。

Python 深度学习 - 基础

在本章中，我们将深入了解 Python 深度学习的基础知识。

深度学习模型/算法

现在让我们学习不同的深度学习模型/算法。

深度学习中的一些流行模型如下 -

• 卷积神经网络
• 循环神经网络
• 深度信念网络
• 生成对抗网络
• 自动编码器等等

输入和输出表示为向量或张量。例如，神经网络的输入可能是图像中各个像素的 RGB 值，表示为向量。

位于输入层和输出层之间的神经元层称为隐藏层。当神经网络尝试解决问题时，大部分工作都在这里发生。仔细观察隐藏层可以揭示网络学习从数据中提取的许多特征。

通过选择将哪些神经元连接到下一层中的其他神经元来形成神经网络的不同架构。

计算输出的伪代码

以下是计算前馈神经网络输出的伪代码 -

• # node[] := 拓扑排序后的节点数组
• # 从 a 到 b 的边表示 a 在 b 的左侧
• # 如果神经网络有 R 个输入和 S 个输出，
• # 则前 R 个节点是输入节点，最后 S 个节点是输出节点。
• # incoming[x] := 连接到节点 x 的节点
• # weight[x] := 连接到 x 的边的权重

从左到右，对于每个神经元 x -

• 如果 x <= R：不做任何操作 # 它是输入节点
• inputs[x] = [output[i] for i in incoming[x]]
• weighted_sum = dot_product(weights[x], inputs[x])
• output[x] = Activation_function(weighted_sum)

训练神经网络

现在我们将学习如何训练神经网络。我们还将学习反向传播算法和 Python 深度学习中的反向传播过程。

我们必须找到神经网络权重的最佳值以获得所需的输出。为了训练神经网络，我们使用迭代梯度下降法。我们最初以权重的随机初始化开始。随机初始化后，我们使用前向传播过程对数据的一部分进行预测，计算相应的成本函数 C，并通过与 dC/dw 成比例的量更新每个权重 w，即成本函数相对于权重的导数。比例常数称为学习率。

可以使用反向传播算法有效地计算梯度。反向传播或反向传播的关键观察结果是，由于微分的链式法则，神经网络中每个神经元的梯度都可以使用其具有传出边的神经元的梯度来计算。因此，我们反向计算梯度，即首先计算输出层的梯度，然后计算最顶层的隐藏层，然后计算前面的隐藏层，依此类推，直到输入层。

反向传播算法主要使用计算图的概念来实现，其中每个神经元都扩展到计算图中的多个节点，并执行简单的数学运算，如加法、乘法。计算图的边上没有任何权重；所有权重都分配给节点，因此权重成为它们自己的节点。然后在计算图上运行反向传播算法。计算完成后，只需要权重节点的梯度进行更新。其余的梯度可以丢弃。

梯度下降优化技术

一个常用的优化函数，根据它们导致的误差调整权重，称为“梯度下降”。

梯度是斜率的另一个名称，而斜率在 x-y 图上表示两个变量之间的关系：上升量除以运行量，距离变化量除以时间变化量等。在本例中，斜率是网络误差与单个权重之间的比率；即，随着权重的变化，误差如何变化。

更准确地说，我们想要找到产生最小误差的权重。我们想要找到正确表示输入数据中包含的信号并将它们转换为正确分类的权重。

随着神经网络的学习，它会缓慢地调整许多权重，以便它们能够正确地将信号映射到含义。网络误差与每个权重之间的比率是一个导数 dE/dw，它计算权重的微小变化导致误差的微小变化的程度。

每个权重只是涉及许多变换的深度网络中的一个因素；权重的信号通过激活并跨多个层求和，因此我们使用微积分的链式法则来回溯网络激活和输出。这将我们引向所讨论的权重，以及它与整体误差的关系。

假设有两个变量，误差（error）和权重（weight），它们由第三个变量**激活（activation）**介导，权重通过激活传递。我们可以通过首先计算激活的变化如何影响误差的变化，以及权重的变化如何影响激活的变化，来计算权重的变化如何影响误差的变化。

深度学习的基本思想不过如此：根据模型产生的误差调整模型的权重，直到无法进一步减少误差。

如果梯度值较小，深度网络训练速度缓慢；如果梯度值较高，训练速度较快。训练过程中的任何不准确性都会导致输出不准确。从输出到输入训练网络的过程称为反向传播或反向传播（back propagation 或 back prop）。我们知道前向传播从输入开始，向前工作。反向传播则相反，从右到左计算梯度。

每次计算梯度时，我们都会使用之前所有计算过的梯度。

让我们从输出层的一个节点开始。该边使用该节点处的梯度。当我们回到隐藏层时，它变得更加复杂。两个介于0到1之间的数字的乘积会得到一个更小的数字。梯度值不断减小，因此反向传播需要大量时间来训练，并且准确性会受到影响。

深度学习算法的挑战

浅层神经网络和深层神经网络都面临着一些挑战，例如过拟合和计算时间。DNNs容易受到过拟合的影响，因为它们使用了额外的抽象层，使它们能够对训练数据中的罕见依赖关系进行建模。

在训练过程中应用**正则化（Regularization）**方法，如dropout、提前停止、数据增强、迁移学习，可以有效对抗过拟合。Dropout正则化在训练期间随机忽略隐藏层中的单元，这有助于避免罕见的依赖关系。DNNs会考虑多个训练参数，例如大小（即层数和每层单元数）、学习率和初始权重。由于时间和计算资源成本高昂，找到最优参数并不总是切实可行的。一些技巧，例如批处理，可以加快计算速度。GPU强大的处理能力极大地帮助了训练过程，因为所需的矩阵和向量计算在GPU上执行效率很高。

Dropout

Dropout是一种流行的神经网络正则化技术。深度神经网络特别容易过拟合。

现在让我们看看什么是Dropout以及它是如何工作的。

用深度学习先驱之一杰弗里·辛顿（Geoffrey Hinton）的话来说，“如果你有一个深度神经网络，它没有过拟合，那么你可能应该使用一个更大的网络并使用Dropout”。

Dropout是一种技术，在梯度下降的每次迭代中，我们都会随机丢弃一组选定的节点。这意味着我们会随机忽略一些节点，就好像它们不存在一样。

每个神经元以概率q保留，并以概率1-q随机丢弃。神经网络中每一层的q值可能不同。对于隐藏层，q值为0.5，对于输入层，q值为0，这种设置在各种任务中表现良好。

在评估和预测期间，不使用Dropout。每个神经元的输出乘以q，以便下一层的输入具有相同的期望值。

Dropout背后的想法如下：在没有Dropout正则化的神经网络中，神经元之间会产生相互依赖关系，这会导致过拟合。

实现技巧

在TensorFlow和Pytorch等库中，Dropout的实现是将随机选择的神经元的输出保持为0。也就是说，虽然神经元存在，但其输出被覆盖为0。

提前停止

我们使用一种称为梯度下降的迭代算法来训练神经网络。

提前停止背后的思想很简单：当误差开始增加时停止训练。这里的误差指的是在验证数据上测量的误差，验证数据是用于调整超参数的一部分训练数据。在这种情况下，超参数是停止标准。

数据增强

我们通过使用现有数据并对其应用一些变换来增加我们拥有的数据量或增强数据。使用的确切变换取决于我们打算实现的任务。此外，有助于神经网络的变换取决于其架构。

例如，在许多计算机视觉任务（如物体分类）中，一种有效的数据增强技术是添加新的数据点，这些数据点是原始数据的裁剪或平移版本。

当计算机接受图像作为输入时，它会接收一个像素值数组。假设整张图像向左移动了15个像素。我们应用许多不同方向的不同偏移量，从而生成一个增强的数据集，其大小是原始数据集的许多倍。

迁移学习

使用预训练模型并用我们自己的数据集“微调”模型的过程称为迁移学习。有几种方法可以做到这一点。下面描述了一些方法：

• 我们使用大型数据集训练预训练模型。然后，我们移除网络的最后一层，并用一个具有随机权重的新层替换它。

• 然后，我们冻结所有其他层的权重，并像往常一样训练网络。这里的冻结层是指在梯度下降或优化过程中不改变权重。

其背后的概念是，预训练模型将充当特征提取器，只有最后一层将在当前任务上进行训练。

计算图

反向传播在Tensorflow、Torch、Theano等深度学习框架中通过使用计算图来实现。更重要的是，理解计算图上的反向传播结合了多种不同的算法及其变体，例如时间反向传播和具有共享权重的反向传播。一旦所有内容都被转换为计算图，它们仍然是相同的算法——只是计算图上的反向传播。

什么是计算图

计算图被定义为一个有向图，其中节点对应于数学运算。计算图是表达和评估数学表达式的途径。

例如，这里有一个简单的数学方程式：

$$p = x+y$$

我们可以绘制上述方程式的计算图如下所示。

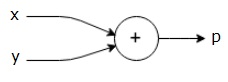
上述计算图有一个加法节点（带“+”号的节点），有两个输入变量x和y，以及一个输出q。

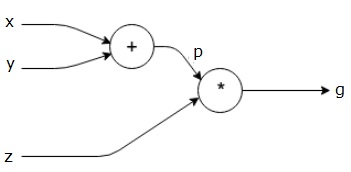
让我们再举一个稍微复杂一点的例子。我们有以下方程式：

$$g = \left (x+y \right ) \ast z $$

上述方程式由以下计算图表示。

计算图和反向传播

计算图和反向传播都是深度学习中训练神经网络的重要核心概念。

前向传递

前向传递是评估计算图表示的数学表达式值的步骤。进行前向传递意味着我们正在将值从变量向前传递，从左侧（输入）到右侧（输出）。

让我们考虑一个例子，为所有输入赋予一些值。假设所有输入都被赋予以下值：

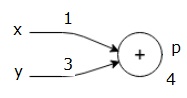
$$x=1, y=3, z=−3$$

通过将这些值赋予输入，我们可以执行前向传递，并获得每个节点上输出的以下值。

首先，我们使用x = 1和y = 3的值，得到p = 4。

然后我们使用p = 4和z = -3得到g = -12。我们从左到右，向前进行。

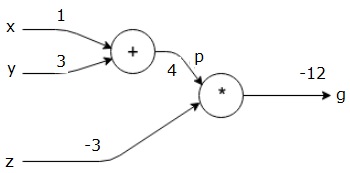
反向传递的目标

在反向传递中，我们的目的是计算每个输入相对于最终输出的梯度。这些梯度对于使用梯度下降训练神经网络至关重要。

例如，我们希望得到以下梯度。

所需的梯度

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

反向传递（反向传播）

我们从求最终输出相对于最终输出本身的导数开始反向传递！因此，它将产生恒等导数，其值等于1。

$$\frac{\partial g}{\partial g} = 1$$

我们的计算图现在如下图所示：

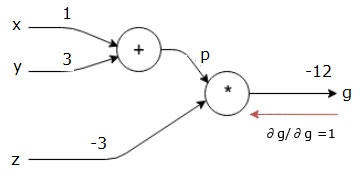
接下来，我们将通过“*”运算进行反向传递。我们将计算p和z处的梯度。由于g = p*z，我们知道：

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

我们已经从前向传递中知道了z和p的值。因此，我们得到：

$$\frac{\partial g}{\partial z} = p = 4$$

以及

$$\frac{\partial g}{\partial p} = z = -3$$

我们想要计算x和y处的梯度：

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

但是，我们希望有效地做到这一点（虽然x和g在这个图中只有两跳远，想象一下它们彼此之间相距很远）。为了有效地计算这些值，我们将使用微分的链式法则。根据链式法则，我们有：

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

但我们已经知道dg/dp = -3，dp/dx和dp/dy很容易计算，因为p直接依赖于x和y。我们有：

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

因此，我们得到：

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

此外，对于输入y：

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

这样向后计算的主要原因是，当我们需要计算x处的梯度时，我们只使用了已经计算过的值，以及dq/dx（节点输出相对于同一节点输入的导数）。我们使用局部信息来计算全局值。

训练神经网络的步骤

按照以下步骤训练神经网络：

• 对于数据集中的数据点x，我们进行前向传递，将x作为输入，并计算成本c作为输出。

• 我们从c开始进行反向传递，并计算图中所有节点的梯度。这包括表示神经网络权重的节点。

• 然后我们通过W = W - 学习率 * 梯度来更新权重。

• 我们重复此过程，直到满足停止条件。

Python深度学习 - 应用

深度学习在一些应用中取得了良好的成果，例如计算机视觉、语言翻译、图像字幕、音频转录、分子生物学、语音识别、自然语言处理、自动驾驶汽车、脑肿瘤检测、实时语音翻译、音乐创作、自动游戏玩耍等等。

深度学习是继机器学习之后更高级的实现，是下一个重大飞跃。目前，它正朝着成为行业标准的方向发展，并有望在处理原始非结构化数据方面成为游戏规则改变者。

深度学习目前是解决各种现实世界问题的最佳解决方案提供商之一。开发人员正在构建人工智能程序，这些程序不是使用预先给定的规则，而是从示例中学习以解决复杂的任务。随着许多数据科学家使用深度学习，更深层的神经网络正在提供越来越准确的结果。

其想法是通过增加每个网络的训练层数来开发深度神经网络；机器学习更多关于数据的信息，直到它尽可能准确。开发人员可以使用深度学习技术来实现复杂的机器学习任务，并训练人工智能网络具有高水平的感知识别能力。

深度学习在计算机视觉领域得到了广泛应用。其中一项取得成功的任务是图像分类，即给定输入图像，将其分类为猫、狗等，或者将其分类为最能描述图像的类别或标签。我们人类在很早的时候就学会了如何执行这项任务，并具备了快速识别模式、从先验知识中归纳以及适应不同图像环境的能力。

库和框架

在本章中，我们将深度学习与不同的库和框架联系起来。

深度学习和Theano

如果我们想开始编写深度神经网络代码，最好了解Theano、TensorFlow、Keras、PyTorch等不同框架的工作原理。

Theano是一个Python库，它提供了一组函数来构建深度网络，这些网络可以在我们的机器上快速训练。

Theano由加拿大蒙特利尔大学在深度网络先驱Yoshua Bengio的领导下开发。

Theano允许我们定义和评估包含向量和矩阵的数学表达式，其中矩阵是数字的矩形数组。

从技术上讲，神经网络和输入数据都可以表示为矩阵，所有标准网络操作都可以重新定义为矩阵操作。这很重要，因为计算机可以非常快速地执行矩阵运算。

我们可以并行处理多个矩阵值，如果我们使用这种底层结构构建神经网络，则可以使用带有GPU的单台机器在合理的时间窗口内训练巨大的网络。

但是，如果我们使用Theano，则必须从头开始构建深度网络。该库没有提供创建特定类型深度网络的完整功能。

相反，我们必须编写深度网络的每个方面，例如模型、层、激活函数、训练方法以及任何用于阻止过拟合的特殊方法。

不过，好消息是Theano允许在向量化函数之上构建我们的实现，从而为我们提供了一个高度优化的解决方案。

还有许多其他库扩展了Theano的功能。TensorFlow和Keras可以使用Theano作为后端。

使用TensorFlow进行深度学习

Google的TensorFlow是一个Python库。对于构建商业级深度学习应用程序来说，这是一个不错的选择。

TensorFlow起源于另一个库DistBelief V2，它是Google Brain项目的一部分。该库旨在扩展机器学习的可移植性，以便将研究模型应用于商业级应用程序。

与Theano库非常相似，TensorFlow基于计算图，其中节点表示持久数据或数学运算，边表示节点之间的数据流，数据流是一个多维数组或张量；因此得名TensorFlow。

来自一个操作或一组操作的输出作为输入馈送到下一个操作中。

尽管TensorFlow是为神经网络设计的，但它也适用于其他网络，在这些网络中，计算可以建模为数据流图。

TensorFlow还使用了Theano的几个特性，例如公共和子表达式消除、自动微分、共享和符号变量。

可以使用TensorFlow构建不同类型的深度网络，例如卷积网络、自动编码器、RNTN、RNN、RBM、DBM/MLP等等。

但是，TensorFlow不支持超参数配置。对于此功能，我们可以使用Keras。

深度学习和Keras

Keras是一个功能强大、易于使用的Python库，用于开发和评估深度学习模型。

它具有极简主义的设计，允许我们逐层构建网络；训练它，并运行它。

它封装了高效的数值计算库Theano和TensorFlow，并允许我们在几行代码中定义和训练神经网络模型。

它是一个高级神经网络API，有助于广泛使用深度学习和人工智能。它运行在许多低级库之上，包括TensorFlow、Theano等等。Keras代码是可移植的；我们可以使用Theano或TensorFlow作为后端在Keras中实现神经网络，而无需更改代码。

Python深度学习 - 实现

在这个深度学习的实现中，我们的目标是预测某家银行的客户流失或客户流失数据 - 哪些客户可能离开这家银行服务。所使用的数据集相对较小，包含10000行和14列。我们使用Anaconda发行版以及Theano、TensorFlow和Keras等框架。Keras构建在Tensorflow和Theano之上，它们充当Keras的后端。

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

步骤1：数据预处理

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

步骤2

我们创建数据集特征和目标变量的矩阵，目标变量是第14列，标记为“Exited”。

数据的初始外观如下所示：

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

输出

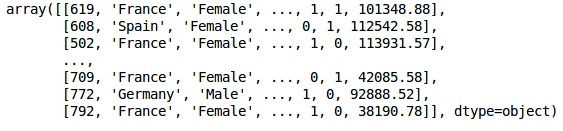
步骤3

Y

输出

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

步骤4

我们通过对字符串变量进行编码来简化分析。我们使用ScikitLearn函数'LabelEncoder'自动对列中的不同标签进行编码，其值为0到n_classes-1。

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

输出

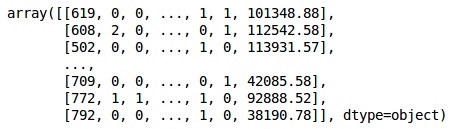
在上面的输出中，国家名称被替换为0、1和2；而男性和女性分别被替换为0和1。

步骤5

标签编码数据

我们使用相同的ScikitLearn库和另一个称为OneHotEncoder的函数，只需传递列号即可创建虚拟变量。

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

现在，前两列表示国家，第4列表示性别。

输出

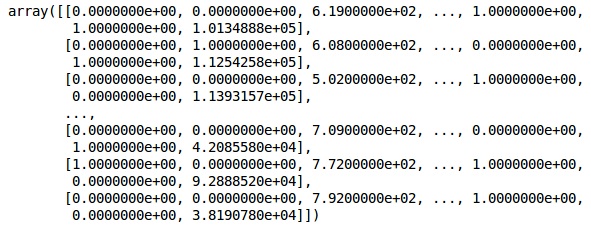
我们总是将数据分成训练和测试部分；我们在训练数据上训练我们的模型，然后我们在测试数据上检查模型的准确性，这有助于评估模型的效率。

步骤6

我们使用ScikitLearn的train_test_split函数将我们的数据分成训练集和测试集。我们将训练与测试的分割比例保持为80:20。

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

有些变量的值以千计，而有些变量的值则以十或一计。我们对数据进行缩放，使其更具代表性。

步骤7

在这段代码中，我们使用StandardScaler函数拟合并转换训练数据。我们标准化我们的缩放，以便我们使用相同的拟合方法来转换/缩放测试数据。

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

输出

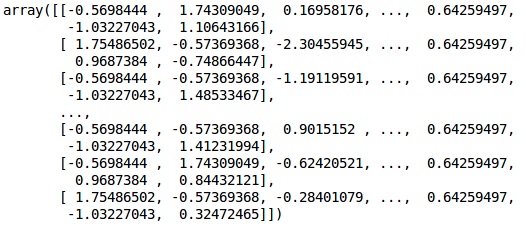
数据现在已正确缩放。最后，我们完成了数据预处理。现在，我们将开始我们的模型。

步骤8

我们在这里导入所需的模块。我们需要Sequential模块来初始化神经网络，以及dense模块来添加隐藏层。

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

步骤9

我们将模型命名为Classifier，因为我们的目标是分类客户流失。然后我们使用Sequential模块进行初始化。

#Initializing Neural Network 
classifier = Sequential()

步骤10

我们使用dense函数逐一添加隐藏层。在下面的代码中，我们将看到许多参数。

我们的第一个参数是output_dim。它是我们添加到此层的节点数。init是随机梯度下降的初始化。在神经网络中，我们为每个节点分配权重。在初始化时，权重应接近于零，我们使用uniform函数随机初始化权重。input_dim参数仅在第一层需要，因为模型不知道我们的输入变量的数量。这里输入变量的总数为11。在第二层，模型会自动从第一隐藏层知道输入变量的数量。

执行以下代码行以添加输入层和第一隐藏层：

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

执行以下代码行以添加第二隐藏层：

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

执行以下代码行以添加输出层：

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

步骤11

编译ANN

到目前为止，我们已经向分类器添加了多个层。我们现在将使用compile方法编译它们。在最终编译中添加的参数控制了整个神经网络的完成。因此，我们必须谨慎地执行此步骤。

以下是参数的简要说明。

第一个参数是Optimizer。这是一种用于找到最佳权重集的算法。该算法称为随机梯度下降（SGD）。这里我们使用几种类型中的一种，称为“Adam优化器”。SGD依赖于损失，因此我们的第二个参数是损失。如果我们的因变量是二元的，我们使用称为'binary_crossentropy'的对数损失函数，如果我们的因变量在输出中有多于两个类别，则我们使用'categorical_crossentropy'。我们希望根据accuracy提高神经网络的性能，因此我们将metrics添加为准确性。

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

步骤12

此步骤需要执行多行代码。

将ANN拟合到训练集

我们现在在训练数据上训练我们的模型。我们使用fit方法来拟合我们的模型。我们还优化权重以提高模型效率。为此，我们必须更新权重。Batch size是在更新权重后观察到的次数。Epoch是迭代的总数。批大小和时期的值是通过试错法选择的。

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

做出预测并评估模型

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

预测单个新的观察结果

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

步骤13

预测测试集结果

预测结果将为您提供客户离开公司的概率。我们将该概率转换为二进制0和1。

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

步骤14

这是我们评估模型性能的最后一步。我们已经有了原始结果，因此我们可以构建混淆矩阵来检查模型的准确性。

创建混淆矩阵

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

输出

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

从混淆矩阵中，可以计算出模型的准确率为：

Accuracy = 1541+175/2000=0.858

我们实现了85.8%的准确率，这是一个不错的结果。

前向传播算法

在本节中，我们将学习如何编写代码以对简单神经网络进行前向传播（预测）：

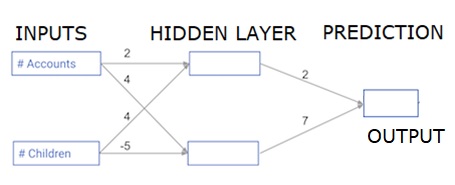
每个数据点都是一个客户。第一个输入是他们有多少个账户，第二个输入是他们有多少个孩子。该模型将预测用户明年将进行多少次交易。

输入数据预先加载为 input_data，权重存储在一个名为 weights 的字典中。隐藏层第一个节点的权重数组位于 weights['node_0'] 中，隐藏层第二个节点的权重数组位于 weights['node_1'] 中。

输出节点的输入权重可在 weights 中获取。

修正线性激活函数

“激活函数”是每个节点都会执行的一个函数。它将节点的输入转换为某种输出。

修正线性激活函数（称为ReLU）广泛应用于高性能网络中。此函数接收一个数字作为输入，如果输入为负数则返回 0，如果输入为正数则返回输入值作为输出。

以下是一些示例：

• relu(4) = 4
• relu(-2) = 0

我们填写 relu() 函数的定义：

• 我们使用 max() 函数计算 relu() 输出的值。
• 我们将 relu() 函数应用于 node_0_input 以计算 node_0_output。
• 我们将 relu() 函数应用于 node_1_input 以计算 node_1_output。

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

输出

0.9950547536867305
-3

将网络应用于多个观测值/数据行

在本节中，我们将学习如何定义一个名为 predict_with_network() 的函数。此函数将根据上述网络作为输入的 input_data 生成多个数据观测值的预测。将使用上述网络中给出的权重。也将使用 relu() 函数的定义。

让我们定义一个名为 predict_with_network() 的函数，它接受两个参数 - input_data_row 和 weights - 并返回网络的预测作为输出。

我们计算每个节点的输入和输出值，并将其存储为：node_0_input、node_0_output、node_1_input 和 node_1_output。

为了计算节点的输入值，我们将相关的数组相乘并计算它们的和。

为了计算节点的输出值，我们将 relu() 函数应用于节点的输入值。我们使用“for 循环”迭代 input_data：

我们还使用我们的 predict_with_network() 为 input_data 的每一行 - input_data_row 生成预测。我们还将每个预测追加到 results 中。

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

输出

[0, 12]

在这里，我们使用了 relu 函数，其中 relu(26) = 26，relu(-13) = 0，依此类推。

深度多层神经网络

在这里，我们正在编写代码来对具有两个隐藏层的神经网络进行前向传播。每个隐藏层有两个节点。输入数据已预先加载为input_data。第一个隐藏层中的节点称为 node_0_0 和 node_0_1。

它们的权重分别预先加载为 weights['node_0_0'] 和 weights['node_0_1']。

第二个隐藏层中的节点称为node_1_0 和 node_1_1。它们的权重分别预先加载为weights['node_1_0'] 和weights['node_1_1']。

然后，我们使用预先加载为weights['output'] 的权重从隐藏节点创建模型输出。

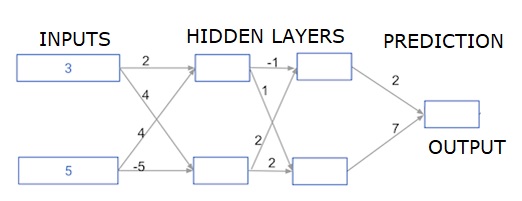
我们使用其权重 weights['node_0_0'] 和给定的 input_data 计算 node_0_0_input。然后应用 relu() 函数以获取 node_0_0_output。

我们对 node_0_1_input 执行与上述相同的操作以获取 node_0_1_output。

我们使用其权重 weights['node_1_0'] 和第一隐藏层的输出 - hidden_0_outputs 计算 node_1_0_input。然后应用 relu() 函数以获取 node_1_0_output。

我们对 node_1_1_input 执行与上述相同的操作以获取 node_1_1_output。

我们使用 weights['output'] 和第二隐藏层 hidden_1_outputs 数组的输出计算 model_output。我们不将 relu() 函数应用于此输出。

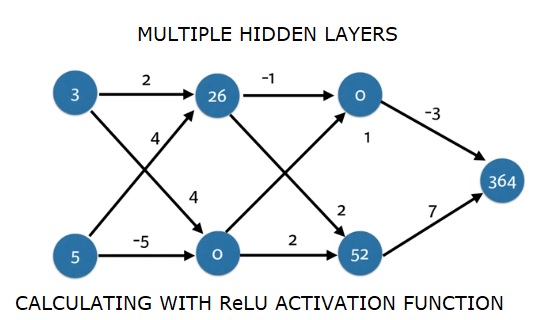
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

输出

364