径向加速度

---

介绍

径向加速度通常出现在外力作用于物体时，根据牛顿第二定律，加速度是物体速度随时间的变化率。它是一个矢量量，既包含大小也包含方向。

径向加速度的测量单位是$\mathrm{ms^{-2}}$。简单来说，径向加速度指的是物体速度与总时间的特定比例。根据物体的两种运动类型，径向加速度也不同。

物体的运动既可以是直线运动也可以是圆周运动。因此，根据运动的不同，物体的加速度也有两种类型：径向加速度和切向加速度。

什么是径向加速度？

径向加速度的符号是a，它会随物体的角速度以及运动方向而不断变化。物体的运动比例、速度以及运动方向被认为是径向加速度。它可以定义为速度相对于特定时间的变化率。

径向加速度被认为是物体指向该物体中心的加速度。这种类型的加速度主要发生在圆周运动中，而物体的运动与物体的半径有关。

径向加速度的单位

物体径向加速度的测量单位有两种：每秒平方弧度和每秒平方米。

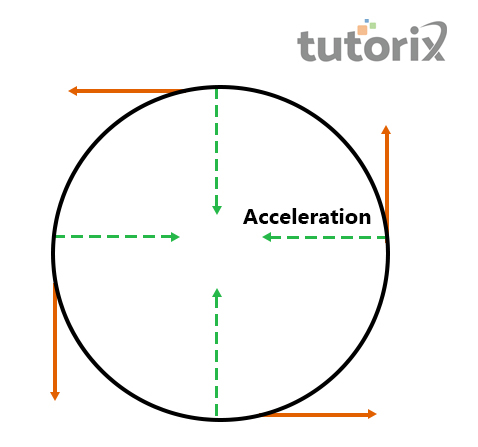
图1：圆周运动

每秒平方弧度用$\mathrm{\omega s^{-2}}$和$\mathrm{ms^{-2}}$表示。物体的角位移单位是弧度，角速度单位是$\mathrm{弧度/秒}$。$\mathrm{弧度/秒^2}$是角加速度的单位。

径向加速度：特征

• 角加速度分为径向加速度和切向加速度两种。

• 径向加速度主要指指向物体中心的物体加速度。

• 当以每秒平方的弧度表示时，径向加速度可以用$\mathrm{\omega s^{-2}}$单位来测量。

• 径向加速度也常被称为向心加速度。

• 切向加速度是指角加速度的主要分量。

• 径向加速度始终可以表示为瞬时速度，因此通常被称为一般加速度。

• 它被称为向心加速度，因为这种类型的加速度主要指向轨迹曲率的瞬时中心。

• 这种类型的运动并非仅定义于圆周运动，而是多种类型的运动。

径向加速度的分量

径向加速度取决于一些影响加速度率的分量。角位移是一种可以定义为物体初始位置和最终位置之间角度差的分量。该分量的符号为𝜃，其公式为$\mathrm{\theta = s/r}$。

角位移的单位是弧度。角速度是另一种类型，可以定义为角位移相对于特定时间的变化率。该分量的符号为⍵，其公式为$\mathrm{\omega = d \theta /dt}$ (Brouwer et al. 2021)。角位移的单位是$\mathrm{弧度/秒}$。角加速度是另一种类型，可以定义为角速度相对于特定时间的变化率 (Stone & Courteau, 2019)。

该分量的符号为$\mathrm{\alpha}$，其公式为$\mathrm{\alpha = \frac{d \omega}{dt}}$。角位移的单位是$\mathrm{弧度/秒^2}$。

径向加速度的公式

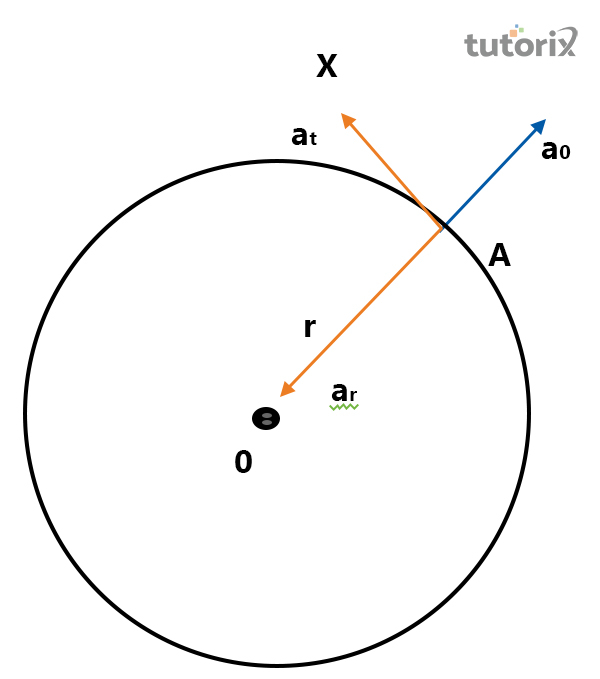
图2：旋转运动物体的示意图

物体A用绳子与另一个物体相连，当它围绕固定点O旋转时，看起来像一个圆形半径。因此，在这种情况下，产生了沿径向方向的a0加速度。

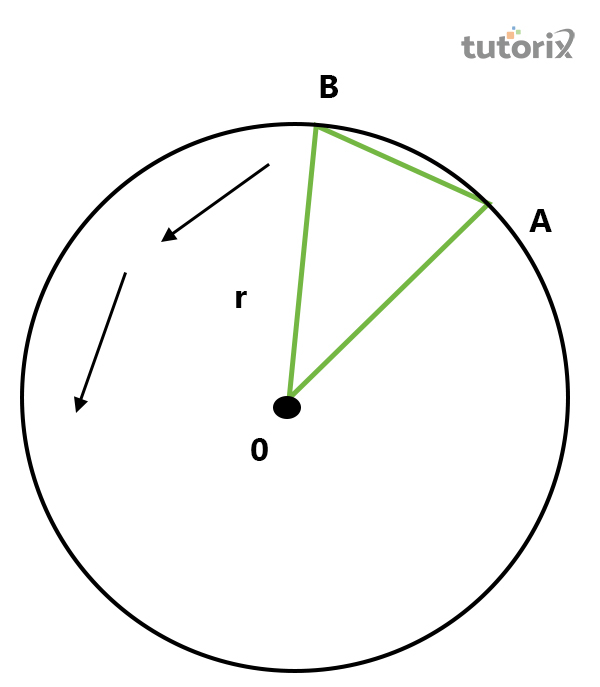
图3：两个物体的径向加速度

对于两个不同的物体，径向加速度可以用公式$\mathrm{AB\:=\:v\:\times\:dt}$来测量，其中A和B是两个物体，它取决于v（表示速度）和dt（表示时间差） (Pradyumna & Desai, 2021)。

如果这两个物体非常接近，则公式变为$\mathrm{v\:+\:dv\:≈\:dv\:\times\:AB/OA}$，也可以表示为$\mathrm{dv/v\:=\:v^2/r}$。对于切向加速度，公式为$\mathrm{at\:=\:v^2-v1/t}$，其中，at表示切向分量，t表示时间段，$\mathrm{v^2}$或$\mathrm{v^3}$表示从圆周运动中获得的两个不同物体的速度结果。

结论

在任何时刻，径向加速度的大小为$\mathrm{v^2/r}$，其中v代表物体的速度，r是任何时刻曲率的半径。在圆周运动中，$\mathrm{r}$指半径，径向加速度的方向与曲率半径相同。在匀速圆周运动(UCM)中，切向加速度始终定义为零，因为物体的速度是相同的。在任何类型的直线运动中，径向加速度始终为零，因为曲率半径在直线上，指的是无限大。

常见问题

Q1. 加速度和减速度是什么？

加速度和减速度都是物体速度的变化。这两个粒子的速率取决于时间。

Q2. 角运动有哪些类型？

角运动有两种不同的类型：径向加速度和切向加速度。这两种类型都取决于速度和时间。

Q.3 什么是角速度？

角位移的时间变化率称为角速度。其公式为$\mathrm{(\omega) = (\delta \theta /\delta t)}$。

Q4. 加速度有哪些类型？

线加速度和圆加速度是两种类型的加速度。沿曲线轨迹运动的物体的物体包含非零径向加速度。