数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中的矩形面积 II
假设我们有一系列（轴对齐的）矩形。这里每个矩形[i] = {x1, y1, x2, y2}，其中 (x1, y1) 是左下角的点，(x2, y2) 是第 i 个矩形的右上角的点。
我们必须找到平面上所有矩形覆盖的总面积。答案可能非常大，所以我们可以使用模 10^9 + 7。
因此，如果输入类似于
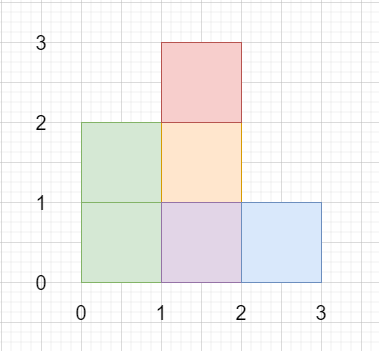
则输出将为 6。
为了解决这个问题，我们将遵循以下步骤 -
m = 10^9 + 7
定义一个函数 add()，它将接收 a、b，
返回 ((a mod m) + (b mod m) mod m)
定义一个函数 compress，它将接收二维矩阵 v
定义一个数组 temp
对于初始化 i := 0，当 i < v 的大小，更新（i 增加 1），执行 -
将 v[i, 0] 插入到 temp 的末尾
将 v[i, 2] 插入到 temp 的末尾
对数组 temp 进行排序
定义一个映射 ret
idx := 0
对于初始化 i := 0，当 i < temp 的大小，更新（i 增加 1），执行
如果 temp[i] 不是 ret 的成员，则 -
ret[temp[i]] := idx
（idx 增加 1）
返回 ret
从主方法执行以下操作 -
定义一个数组 xv
将 { 0 } 插入到 xv 的末尾
对于初始化 i := 0，当 i < v 的大小，更新（i 增加 1），执行 -
将 v[i, 0] 插入到 xv 的末尾
将 v[i, 2] 插入到 xv 的末尾
对数组 xv 进行排序
uniItr = 包含 xv 的唯一元素的列表的第一个元素
从 xv 中删除 uniItr
定义一个映射 index
idx := 0
对于初始化 i := 0，当 i < xv 的大小，更新（i 增加 1），执行 -
index[xv[i]] := i
定义一个大小与 index 大小相同的数组 count
定义一个二维数组 x
对于初始化 i := 0，当 i < v 的大小，更新（i 增加 1），执行 -
x1 := v[i, 0], y1 := v[i, 1]
x2 := v[i, 2], y2 := v[i, 3]
将 { y1, x1, x2, 1 } 插入到 x 的末尾
将 { y2, x1, x2, -1 } 插入到 x 的末尾
对数组 x 进行排序
ret := 0
sum := 0, currentY := 0
对于初始化 i := 0，当 i < x 的大小，更新（i 增加 1），执行 -
y := x[i, 0]
x1 := x[i, 1], x2 := x[i, 2]
sig := x[i, 3]
ret := add(ret, (y - currentY) * sum)
currentY := y
对于初始化 i := index[x1]，当 i < index[x2]，更新（i 增加 1），执行 -
count[i] := count[i] + sig
sum := 0
对于初始化 i := 0，当 i < count 的大小，更新（i 增加 1），执行 -
如果 count[i] > 0，则
sum := sum + (xv[i + 1] - xv[i])
返回 ret mod m
让我们看看以下实现以更好地理解 -
示例
#include <bits/stdc++.h>
using namespace std;
typedef long long int lli;
const int m = 1e9 + 7;
class Solution {
public:
lli add(lli a, lli b){
return ((a % m) + (b % m) % m);
}
map<int, int> compress(vector<vector<int> >& v){
vector<int> temp;
for (int i = 0; i < v.size(); i++) {
temp.push_back(v[i][0]);
temp.push_back(v[i][2]);
}
sort(temp.begin(), temp.end());
map<int, int> ret;
int idx = 0;
for (int i = 0; i < temp.size(); i++) {
if (!ret.count(temp[i])) {
ret[temp[i]] = idx;
idx++;
}
}
return ret;
}
int rectangleArea(vector<vector<int> >& v){
vector<int> xv;
xv.push_back({ 0 });
for (int i = 0; i < v.size(); i++) {
xv.push_back(v[i][0]);
xv.push_back(v[i][2]);
}
sort(xv.begin(), xv.end());
vector<int>::iterator uniItr = unique(xv.begin(), xv.end());
xv.erase(uniItr, xv.end());
map<int, int> index;
int idx = 0;
for (int i = 0; i < xv.size(); i++) {
index[xv[i]] = i;
}
vector<int> count(index.size());
vector<vector<int> > x;
int x1, x2, y1, y2;
for (int i = 0; i < v.size(); i++) {
x1 = v[i][0];
y1 = v[i][1];
x2 = v[i][2];
y2 = v[i][3];
x.push_back({ y1, x1, x2, 1 });
x.push_back({ y2, x1, x2, -1 });
}
sort(x.begin(), x.end());
lli ret = 0;
lli sum = 0, currentY = 0;
for (int i = 0; i < x.size(); i++) {
lli y = x[i][0];
x1 = x[i][1];
x2 = x[i][2];
int sig = x[i][3];
ret = add(ret, (y - currentY) * sum);
currentY = y;
for (int i = index[x1]; i < index[x2]; i++) {
count[i] += sig;
}
sum = 0;
for (int i = 0; i < count.size(); i++) {
if (count[i] > 0) {
sum += (xv[i + 1] - xv[i]);
}
}
}
return ret % m;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,0,2,2},{1,0,2,3},{1,0,3,1}};
cout << (ob.rectangleArea(v));
}输入
{{0,0,2,2},{1,0,2,3},{1,0,3,1}}输出
6
344 次查看
