矩形棱锥

---

简介

矩形棱锥是一种三维立体图形，具有矩形底面和四个三角形平面。根据底面的形状和三角形面的数量，棱锥有很多种类型，例如正方形棱锥、三角形棱锥、五边形棱锥和六边形棱锥。

棱锥的表面是具有直线的平面图形，也可以称为多边形。

如果一个立体图形由多边形构成，则称为多面体。矩形棱锥，或一般意义上的棱锥，都是多面体。棱锥的一种常见类型是矩形棱锥。埃及的金字塔可以作为矩形棱锥的现实例子。埃及人是最早测量棱锥体积的人。

在本教程中，我们将学习如何在不同场景下计算矩形棱锥的表面积和体积。

矩形棱锥

具有五个顶点和八条直线，形成四个三角形表面和一个矩形底面的立体图形称为矩形棱锥。

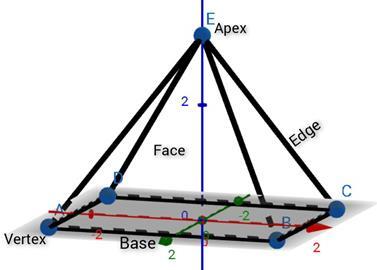
• 连接所有三角形表面的顶部尖端或点被称为矩形棱锥的顶点。

• 其余的点或角，作为边其他端点的交点，是顶点。

• 由侧面交点形成的直线是棱。

• 图形的底面和其他表面是面。

表面积公式

当我们探索矩形棱锥的表面积时，我们需要考虑总表面积和侧表面积。

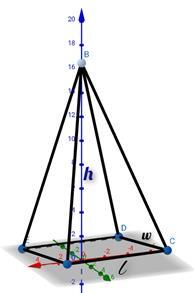
矩形棱锥的总表面积

侧表面积和底面积之和是矩形棱锥的总表面积或 TSA。

公式如下：

$$\mathrm{T.S.A\:=\:lw\:+\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

其中 l 为底边长

w 为底边宽

h 为棱锥的高度

矩形棱锥的侧表面积

不包括底面积的所有侧三角形面的面积之和是矩形棱锥的侧表面积或 LSA。

公式如下：$$\mathrm{L.S.A\:=\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

其中 l 为底边长

w 为底边宽

h 为棱锥的高度

矩形棱锥体积公式

矩形棱锥的体积是通过将底面积 B 乘以棱锥的垂直高度 h 来计算的。

公式如下

$\mathrm{volume\:V\:=\:\frac{1}{3}\times\:base\:are\:\times\:perpendicular\:height}$

$\mathrm{V\:=\:\frac{1}{3}\:Bh}$

$\mathrm{V\:=\:\frac{1}{3}\times\:l\times\:w\times\:h}$

其中底面积 B 为 lw

l 为底边长

w 为底边宽

h 为棱锥的垂直高度。

例题

1)在文员的办公桌上有一个纸镇，形状为矩形棱锥，高 5 厘米，底宽 4 厘米，底长 6 厘米。求纸镇的总表面积。

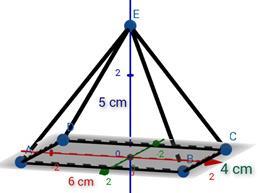
答案 −

矩形棱锥的总表面积

$$\mathrm{=\:lw\:+\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

纸镇的总表面积

$$\mathrm{=\:6\times\:4\:+\:6\sqrt{[(\frac{4}{2})^{2}\:+\:5^{2}]}\:+\:4\sqrt{[(\frac{l}{2})^{2}}\:+\:5^{2}]\:=\:79.63\:cm^{2}}$$

2)假设一块木头被雕刻成一个矩形棱锥，其高度、宽度和长度均为 7 厘米。求这块木头的侧表面积。

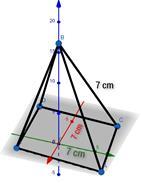
答案 − 矩形棱锥的侧表面积

$$\mathrm{=\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

木头的侧表面积

$$\mathrm{=\:7\sqrt{[(\frac{7}{2})^{2}\:+\:7^{2}]}\:+\:7\sqrt{[(\frac{l}{2})^{2}}\:+\:7^{2}]}$$

$$\mathrm{=\:109.57\:cm^{@}}$$

3)一群 26 个朋友在篝火旁露营。他们在篝火旁搭建了一个大型帐篷，形状为矩形棱锥，底面积为 300 𝒇𝒕𝟐，垂直高度为 30 英尺。求帐篷的体积。

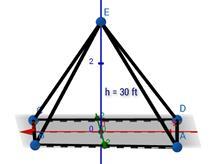
答案 −

$\mathrm{矩形棱锥体积\:=\:\frac{1}{3}\times\:底面积\:\times\:垂直高度}$

$\mathrm{帐篷体积\:=\:\frac{1}{3}\times\:300\times\:30}$

$\mathrm{=\:3000\:ft^{3}}$

4)X 为他的宠物狗建造了一个狗窝，屋顶形状为矩形棱锥，垂直高度为 20 厘米，底面积为 1800 𝒄𝒎𝟐。求屋顶的体积。

答案 −

矩形棱锥的体积 $\mathrm{=\:\frac{1}{3}\:Bh}$

帐篷的体积 $\mathrm{=\:\frac{1}{3}\times\:1800\times\:20}$

$\mathrm{=\:1.2\times\:10^{5}\:cm^{3}}$

5)假设一个矩形棱锥的体积为 2000 𝒄𝒎𝟑，底面积为 240 𝒄𝒎𝟐。求棱锥的垂直高度。

答案 −

矩形棱锥的体积 $\mathrm{=\:\frac{1}{3}\times\:底面积\times\:垂直高度}$

$\mathrm{2000\:=\:\frac{1}{3}\times\:240\times\:h}$

$\mathrm{600\:=\:24\times\:240\times\:h}$

$\mathrm{100\:=\:4\times\:h}$

$\mathrm{h\:=\:25\:cm}$

6)假设矩形棱锥的高度为 12 厘米，体积为 1800 𝒄𝒎𝟑。求棱锥的底面积。

答案 −

矩形棱锥的体积 $\mathrm{=\:\frac{1}{3}\times\:底面积\:\times\:垂直高度}$

$\mathrm{1800\:=\:\frac{1}{3}\:\times\:B\times\:12}$

$\mathrm{5400\:=\:B\times\:12}$

$\mathrm{1800\:=\:B\times\:4}$

$\mathrm{底面积\:B\:=\:450\:cm^{2}}$

结论

• 具有四个三角形面和一个矩形底面的立体图形称为矩形棱锥。

• 矩形棱锥的底面积是其长和宽的乘积。

• 矩形棱锥的总表面积是通过将侧表面积和底面积相加来计算的。

• 矩形棱锥的侧表面积是通过将所有三角形面的面积相加来计算的。

• 矩形棱锥的体积是通过将其底面积乘以其垂直高度来计算的。

常见问题

1. 什么是棱锥？请举一个现实生活中的例子？

通过连接底面和侧三角形面形成的立体图形称为棱锥。

“棱锥”一词来源于希腊语，意思是小麦饼，因为希腊人过去常常将埃及的建筑物比作尖尖的小麦饼。

埃及吉萨大金字塔是一个合适的例子。

2. 什么是正方形棱锥？

. 具有四个三角形面和一个正方形底面的立体图形称为正方形棱锥。它也被称为五面体，因为它有五个面。

3. 正方形棱锥和矩形棱锥有什么区别？

正方形棱锥和矩形棱锥的区别在于底面积，但正方形棱锥可以被称为矩形棱锥，因为它的表面积和体积与矩形棱锥相同，但反之则不然。

4. 什么是三角形棱锥？

具有三个三角形面和一个三角形底面的几何立体图形称为三角形棱锥。

5. 如何测量正方形棱锥的体积？

正方形棱锥的体积与矩形棱锥相同，它是通过将底面积和棱锥高度的乘积的三分之一来计算的。