正六边形

---

引言

如果一个多边形具有相等的二维封闭形状，并且所有多边形的边和内角都相等，则它们被称为正多边形。正方形和等边三角形是正多边形的一些例子。正六边形是一个封闭形状的多边形，它有六条相等的边和六个相等的角。在本教程中，我们将学习正六边形、正六边形的角、正六边形的外部角、正六边形的对角线和对称线、六边形平铺、现实生活中的六边形以及一些相关的已解决示例。

正六边形

“六边形”一词，“hex”意为六，“gonia”意为角，六边形可以定义为二维几何中的六边形。正六边形是一个六边形，它具有六条等长的边和相等的内角。正六边形由六个等边三角形组成。正六边形是一个二维图形，它有六条边、六个内角和六个顶点。蜂窝、地板砖和钟表是正六边形的一些例子。

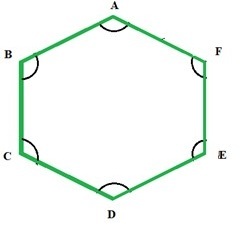
六边形的角

六边形有两種類型的角：内角和外角。正六边形有六个内角和六个外角。正六边形所有内角的和为 720°，所有外角的和为 360°。

由于正多边形的角都相等，因此正六边形的每个角都可以通过 720° ÷ 6 = 120° 计算得出。类似地，正六边形的外部角可以通过 360° ÷ 6 = 60° 计算得出。

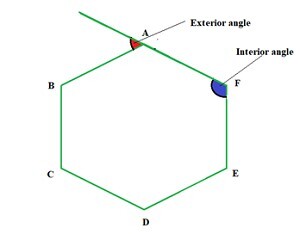
六边形的外角

如图所示，如果正六边形的一条边延伸，它与六边形的相邻边构成一个角，这样的角称为六边形的外角。

正六边形的外角计算方法为：

外角 = 所有外角之和 / 6。

= 360°/6

= 60°

因此，正六边形的外角为 60°。

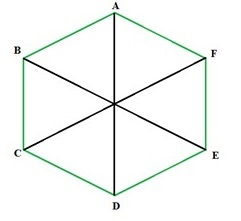
六边形对角线的数量

对角线是在封闭形状图形上连接彼此相对顶点的线。正六边形的对角线也可以类似地绘制。正六边形有九条对角线，对应六个顶点。当绘制所有对角线时，它们将正六边形分成六个等边三角形。如图所示，对角线在中心形成 60 度角。

多边形的对角线数量可以通过公式 n(n-3)/2 计算。

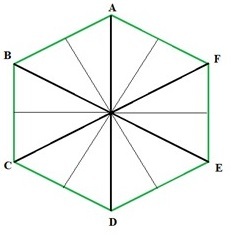
六边形的对称线

对称线可以定义为穿过图形中心并将图形分成两个相同部分的线。如图所示，当为正六边形绘制对称线时，得到六条对称线。

正六边形周期性地平铺平面

欧几里得平面的六边形平铺可以定义为一个正平铺，其中一个顶点由三个六边形共享。我们可以通过将 360 除以多边形的内角（在本例中为 120 度）来确定这一点。欧几里得平面的正平铺可以通过三种方式完成，即通过等边三角形、正方形和正六边形。六边形平铺具有 6 重对称性，即六边形平铺可以旋转 60^o 6 次，并且平铺始终看起来与原始平铺相似。六边形平铺，也称为六边形镶嵌，由著名数学家约翰·康威命名为六边形。

现实生活中的六边形

我们可以在自然界和人工结构中看到六边形图案。当我们平铺平面时，六边形结构彼此契合，没有任何缝隙。因此，蜂窝的细胞是六边形的，因为六边形形状可以有效地利用空间。在化合物的结构中，石墨烯具有六边形网状晶体结构。另一个化合物的例子是苯，它是一种具有六边形分子结构的碳化合物，被认为是化学中最强的结构之一。六边形形状也已用于宇宙学，例如詹姆斯·韦伯太空望远镜，它具有 18 个六边形镜面段，以捕捉尽可能多的光线来观察宇宙中遥远的恒星。

已解决的示例

1.如果正六边形的一条边长为 6 个单位，则计算其面积。

解答

我们知道：

正六边形的面积由 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$ 平方单位给出，其中 s 表示边的单位长度。

已知，边 s = 6 个单位。

因此，面积 $\mathrm{A=\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{A=\frac{3\sqrt{3} 6^2}{2}}$$

= 54√3 平方单位。

因此，正六边形的面积为 54√3 平方单位。

2.如果正六边形的面积为 72√3 平方单位，则求其每条边的长度。

解答

正六边形的面积由 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$ 平方单位给出，其中 s 表示边的单位长度。

因此，$\mathrm{72\sqrt{3}=\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{72=\frac{3}{2} s^2}$$

72×2 = 3s²

48 = s²

s = 4√3

因此，六边形的边长为 4√3。

结论

如果一个多边形具有相等的二维封闭形状，并且所有多边形的边和内角都相等，则它们被称为正多边形。正六边形是一个封闭形状的多边形，它有六条相等的边和六个相等的角。“六边形”一词，“hex”意为六，“gonia”意为角。正多边形有六个内角和六个外角。正六边形所有内角的和为 720 度，所有外角的和为 360 度。每个正六边形有九条对角线。当为正六边形绘制对称线时，得到六条对称线。

常见问题

1. 正六边形的周长是多少？

正六边形的周长可以通过将正六边形的边长乘以 6 来计算。

2. 定义正六边形的内角和外角。

正六边形的内角为 120 度，外角为 60 度。

3. 正六边形的现实生活中的例子是什么？

在雪花显微照片以及蜂窝结构中可以看到正六边形。

4. 六边形与等边三角形有什么关系？

正六边形由六个等边三角形组成，可以通过连接正六边形的对角线来绘制。

5. 正多边形有多少条对称线？

正六边形有 6 条对称线。