一个正六边形内接于一个圆。如果正六边形的面积是\( 24 \sqrt{3} \mathrm{~cm}^{2} \)，求圆的面积。（使用\( \pi=3.14 \)）

已知

一个正六边形内接于一个圆。

正六边形的面积为\( 24 \sqrt{3} \mathrm{~cm}^{2} \)。

要求：

我们必须找到圆的面积。

解答

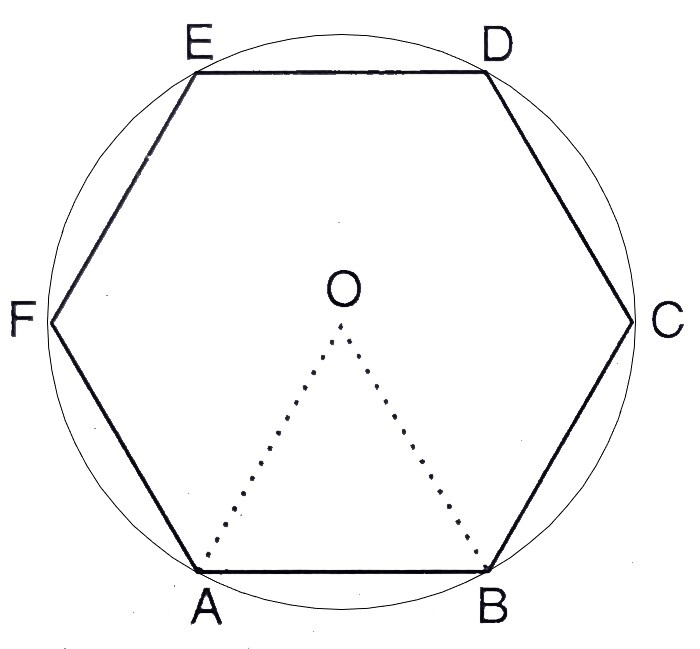
设ABCDEF为正六边形，O为圆心。

连接六边形的顶点与O，得到六个相等的等边三角形。

设圆的半径 = 等边三角形AOB的边长 = r

六边形的面积 = 24√3 cm²

这意味着：

6 × (√3/4) r² = 24√3

=> r² = (24√3 × 4) / (6√3)

=> r² = 16

圆的面积 = πr²

= 3.14 × 16

= 50.24 cm²

圆的面积是50.24 cm²。

教程点

更新于：2022年10月10日

175次浏览

开启你的职业生涯

完成课程获得认证

开始学习