六边形面积公式

---

简介

六边形的面积是由其所有边围成的空间。六边形是一个具有六条边和六个角的多边形。正六边形由六个等边三角形组成，具有六条相等的边和六个相等的角。计算六边形面积的方法有很多，无论是形状不规则的六边形还是正六边形。

计算六边形面积公式的方法有很多。各种方法主要取决于你如何分割六边形。它可以被分成6个等边三角形或2个三角形和1个矩形。在本教程中，我们将讨论六边形面积公式。

六边形

• 六边形是由六条直线组成的封闭二维形状。它在二维空间中具有六条边、六个顶点和六个内角。

• 六边形形状的现实世界例子包括：六角形地砖、铅笔横截面、钟表、蜂窝等。它可以是正六边形（六条边长和角度相等）或不规则六边形（6条边长和角度不相等）。

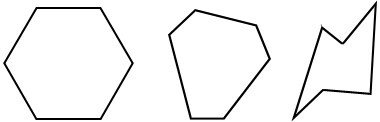
• 正六边形

  正六边形是一个封闭的二维形状，具有六条相等的边和六个相等的角。每个正六边形的角度为120度。

  所有内角的总和为 120 x 6 = 720 度。对于外角，我们知道任何多边形的外角之和始终为 360°。六边形有六个外角。

  因此，正六边形的每个外角为 $\mathrm{\frac{360}{6} = 60}$ 度。

正六边形与不规则六边形的区别在于，不规则六边形的角度和边长没有确定的测量值，并且边长不同。不规则六边形和正六边形共有的某些属性如下：

• 两者都有六条边、六个内角和六个顶点。

• 所有六个内角加起来等于 720 度。

• 所有六个外角加起来等于 360 度。

六边形的面积

• 六边形的面积是由六边形的边围成的区域。

  正六边形的面积为 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$

  其中 s 是六边形边的长度。因为我们讨论的是正六边形，所以所有边的长度都相同。

  当已知正六边形的一条边的长度时，可以使用以下公式计算面积：

• 已知旁心距的六边形面积计算公式为：面积 = $\mathrm{\frac{1}{2} × 周长 × 旁心距}$。

通过将六边形分成三角形来计算面积

边边边规则确保六边形内的所有三角形都全等；每个三角形有两条边在六边形内部，以及构成六边形周长的底边。同样，所有三角形的角度都相同。

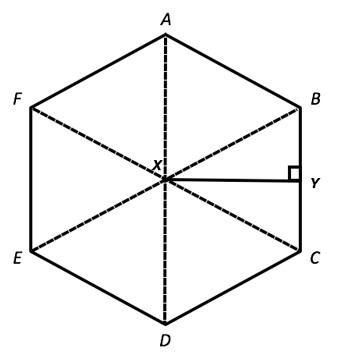
因此，六边形的面积将表示为 ${\mathrm{6×\frac{\sqrt{3} s^2}{4}}}$

$$\mathrm{ =\frac{3\sqrt{3} s^2}{2}}$$

正六边形的面积为 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六边形边的长度。

例题

1) 如果每条边的长度为 4，则求六边形的面积。

答案：已知每条边的长度为 4，我们知道正六边形的面积为 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六边形边的长度。

正六边形的面积=$\mathrm{ \frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{ \frac{3\sqrt{3} \times 4^2}{2}}$$

$$\mathrm{=24\sqrt{3}}$$

2) 如果每条边的长度为 2，则求六边形的面积。

答案：已知每条边的长度为 2，我们知道正六边形的面积为 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六边形边的长度。

正六边形的面积=$\mathrm{ \frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{ \frac{3\sqrt{3} \times 2^2}{2}}$$

$$\mathrm{=6\sqrt{3}}$$

3) 如果六边形的周长为 24，旁心距为 3，则求六边形的面积。

我们知道已知旁心距的六边形面积计算公式。简而言之，

$$\mathrm{面积 =\frac{1}{2} × 24 ×3.}$$

$$\mathrm{=36}$$

4) 如果六边形的周长为 4，旁心距为 1，则求六边形的面积。

答案：已知周长为 4，旁心距为 1。

我们知道已知旁心距的六边形面积计算公式。简而言之，

$$\mathrm{面积 =\frac{1}{2}× 周长 ×旁心距.}$$

$$\mathrm{面积 =\frac{1}{2}× 4 ×1.}$$

$$\mathrm{=2}$$

5) 如果六边形的面积为 20，旁心距为 4，则求六边形的周长。

答案：已知六边形的面积为 20，旁心距为 4。

现在使用关系式，$\mathrm{面积 =\frac{1}{2}× 周长 ×旁心距.}$

$$\mathrm{20 =\frac{1}{2}\times 周长 \times 4}$$

$$\mathrm{\Rightarrow 周长=10}$$

6) 如果六边形的面积为 100，旁心距为 8，则求六边形的周长。

答案：已知六边形的面积为 100，旁心距为 8。

现在使用关系式，$\mathrm{面积 =\frac{1}{2}× 周长 ×旁心距.}$

$$\mathrm{100 =\frac{1}{2}× 周长 ×8.}$$

$$\mathrm{\Rightarrow 周长=25}$$

7) 如果已知面积为 6√3，则求正六边形的边长。

答案：已知六边形的面积为 6√3。

现在使用正六边形面积关系式=$\mathrm{\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{s=2}$$

8) 如果已知面积为 3√3，则求正六边形的边长。

答案：已知六边形的面积为 3√3。

现在使用正六边形面积关系式=$\mathrm{\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{3\sqrt{3}=\frac{3\sqrt{3} s^2}{2}}$$

$$\mathrm{s=\sqrt{2}}$$

结论

六边形是一个六边多边形，有六个角。它源于希腊词“Hexa”（六）和“gon”（角）。

正六边形的面积为 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$，其中 s 是六边形边的长度。

常见问题

1. 六边形是什么意思？

六边形是由六条直线组成的封闭二维形状。它在二维空间中具有六条边、六个顶点和六个内角。

2. 求六边形面积的公式是什么？

求六边形面积的公式是 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$。

3. 六边形的角度是多少？

六边形所有六个内角之和为 720 度。正六边形的每个内角为 120 度。

4. 正六边形到底是什么？

正六边形是一种六边形，其所有边都相等。此外，正六边形的所有六个角都相等。

5. 不规则六边形到底是什么？

与其他边和角相比，不规则六边形至少有一条边和一个角不相等。每个角没有确定的测量值，但所有六个内角之和始终为 720 度，所有六个外角之和为 360 度。

6. 正六边形有多少条对称线？

所有正多边形的对称线数量等于边的数量。因此，正六边形有六条对称线。