逃逸速度与轨道速度的关系

---

简介

本教程旨在解释物理学概念，例如逃逸速度和轨道速度，并解释这两个概念之间的关系。教程将进一步包含逃逸速度和轨道速度的定义，以便建立或举例说明这两个概念之间形成的关系。此外，本教程将包括关系公式的解释以及这两个概念之间存在的差异。

什么是逃逸速度？

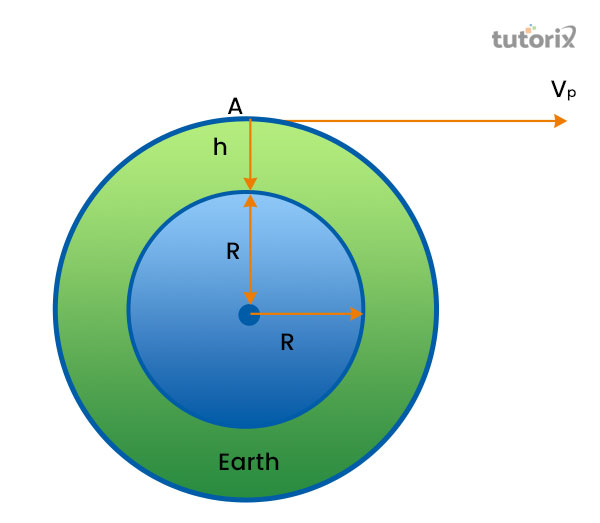
图1：逃逸速度

简单来说，逃逸速度可以定义为一个绕轨道运行的物体为了逃离其正在旋转的轨道而所需的最小速度(Vlacic, 2019)。

对于一个自由的非推进物体，在天体力学术语中，所需最小速度被称为该物体的逃逸速度。物体的逃逸速度通常取决于物体的质量和大小(Drolshagen et al. 2020)。

用于表示逃逸速度的单位是米每秒。这在太空探索中可以看到，因为航天器需要这个逃逸速度才能超越地球的引力。

什么是轨道速度？

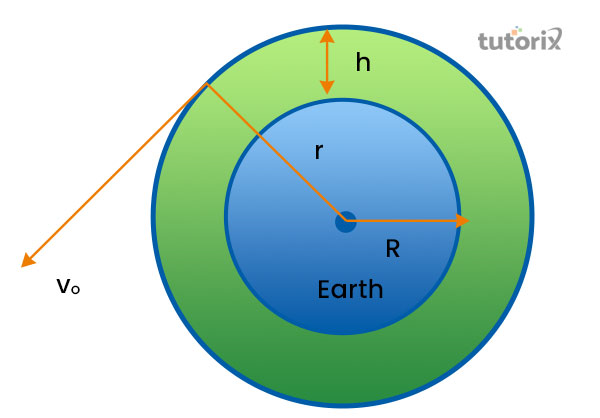
图2：轨道速度

轨道速度可以被解释为一个受引力约束系统的方面，其中一个物体需要一定数量的速度，这被认为是保持轨道所需的足够量(Sciencedirect, 2022)。

为了保持运动，物体可能会受到惯性的影响，即保持运动的趋势，这可能会影响轨道的路径，使其变成直线。在这种情况下，为了避免惯性的影响，物体需要一个最小速度来保持在轨道路径上。

轨道速度的应用体现在天然或人造星光的形状和轨道上，它们将保持在太空中的行星轨道上。轨道速度的依赖性是物体的半径以及物体离表面的高度。

逃逸速度和轨道速度的区别

逃逸速度和轨道速度的概念在它们之间存在一些差异。确定的核心区别是，逃逸速度被解释为物体离开其旋转下方的引力所需的最小速度。另一方面，轨道速度是指物体为了保持轨道，同时保持其速度和与引力物体的距离所需要的速度 GMR = v_o² (Geiger, 2019)。

逃逸速度的公式表示为

v_e = √(2GMR)

相反，轨道速度的公式为v_e = √(GMR/(R+h))。根据逃逸速度数学公式的表达，它也可以表示为√(2gR)。相反，轨道速度的表示也可以通过公式GMR = v_o²来完成。

逃逸速度和轨道速度：关系

轨道速度和逃逸速度之间存在的关系是这两个方面的值彼此成正比。这种说法的意思是，如果物体的轨道速度增加，逃逸速度的值也会增加。同样，如果物体的轨道速度降低，逃逸速度的值也会降低。基于这两个概念性的想法，定义这两种情况的公式是

$$V_{o}= \sqrt{gR} \:and\: V_{e} = \sqrt{2gR}$$

逃逸速度和轨道速度之间关系的公式

第一个等式$V_{o}= \sqrt{gR}$表示轨道速度，第二个公式$V_{e} = \sqrt{2gR}$负责表示逃逸速度。在这两个公式中，字母g指加速度，R指半径的表示，可以形成的主要公式是$V_{e} = \sqrt2 \sqrt{gR}$ (Haug, 2021)。通过代入$V_{o}= \sqrt{gR}$，可以得到$V_{e} = \sqrt2V_{o}$。基于此，轨道速度的值可以通过公式$V_{o} = V_{e} /\sqrt2$找到。

结论

本教程阐明了逃逸速度的定义，在此之后，教程进一步包含了轨道速度的定义以及这两个天体物理学概念化方面之间存在的关系。这两个概念之间存在的关系形成了一个数学公式，该公式指出逃逸速度的值等于√2*轨道速度。这个公式定义了两个形成的关系，说明逃逸速度值的增加或减少对轨道速度的估值产生类似的影响。

常见问题

问1. 逃逸速度和轨道速度是如何相关的？

物体的逃逸速度是根据轨道速度计算的，因为引力控制着轨道速度的增加或减少。考虑到这种情况，形成的公式指出逃逸速度的值等于轨道速度和2的平方根的乘积。

问2. 太阳系中哪个行星拥有最高的逃逸速度？

在太阳系中，木星是唯一一个拥有最高逃逸速度的行星，为每秒59.5公里。

问3. 轨道速度和重力之间有什么关系？

万有引力的平方根共享一个值，该值相当于一个物体的轨道值，该值被认为与物体的质量成正比，与轨道半径成反比。

问4. 逃逸速度取决于哪些因素？

物体的逃逸速度通常取决于物体的两个属性：物体的尺寸及其质量。

参考文献

期刊

Drolshagen, E., Ott, T., Koschny, D., Drolshagen, G., Schmidt, A. K., & Poppe, B. (2020). Velocity distribution of larger meteoroids and small asteroids impacting Earth. Planetary and Space Science, 184, 104869. Retrieved from: https://arxiv.org/pdf/2011.07775

Geiger, J. (2019). Measurement Quantization Describes Galactic Rotational Velocities, Obviates Dark Matter Conjecture. Journal of High Energy Physics, Gravitation and Cosmology, 5(02), 473. Retrieved from: https://www.scirp.org/html/13-2180374_91777.htm

Haug, E. G. (2021). New full relativistic escape velocity and new Hubble related equation for the universe. Physics Essays, 34(4), 502-514. Retrieved from: https://hal.archives-ouvertes.fr/hal-03240114/document

Vlacic, N. (2019). Escape Velocity. Undergraduate Journal of Mathematical Modeling: One+ Two, 3(1), 24. Retrieved from: https://scholar.archive.org

网站

Sciencedirect.com, (2022). Orbital Velocity - an overview Retrieved from: https://www.sciencedirect.com/topics/physics-and-astronomy/orbital-velocity [检索于2022年6月11日]