群速度和相速度之间的关系

---

简介

在本教程中，将讨论有关波的特性（例如相速度和群速度）的信息，并辅以适当的示例。在物理学中，波可以定义为在平面表面上识别的单纯扰动。

基于此概念，本教程将讨论群速度和相速度的定义。此外，本教程还将包括这两个波特性之间共享的关系和差异。

什么是群速度？

图 1：群速度

波的群速度可以解释为在空间中传播时表现出波振幅的整体包络形状的速度。根据量子物理学的术语，通过具有不同振幅和数量的不同波获得“波包”（Sciencedirect，2022）。

• 该粒子的速度被认为等同于发展“波包”的波群。

• 波群的速度由数学表达式“v_g= dω/dk”表示，它表示粒子运动的速度。

相速度的定义

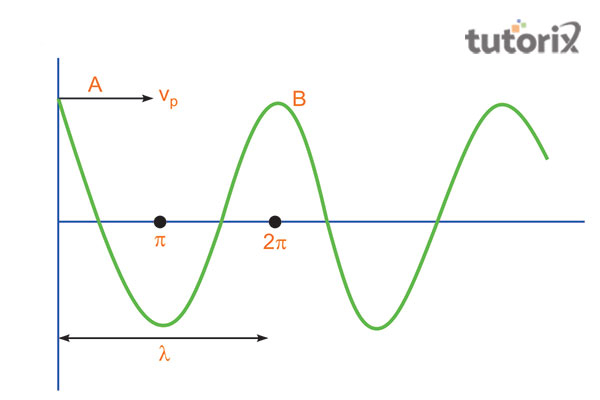
图 2：相速度

波在穿过光谱或任何波包时其相位的速度。例如，可以根据上图得出，其中波的 A 点以“相速度”传播，可以用数学表示为“v_p=ωk”（Jin & Gaherty，2019）。

为了建立这种数学表示，考虑角频率也很重要，它由“ω = 2π f”表示。此方程与角波数相关，角波数由“k = 2π / λ”表示，其中频率和波长分别由 f 和 λ 表示。

相速度和群速度之间的差异

在“反常”介质中，相速度低于“群速度”，而如果波穿过正常介质，则“相速度”的值大于“群速度”。在用波表示粒子的情况下，“群速度”具有更大的重要性，而在处理单个波时，“相速度”具有这种重要性（Yu et al. 2019）。

然而，在“波包”中，已经观察到包络以“波群”的速度传播。相反，已经观察到载波以“相速度”在波包中传播。基于这些矛盾，这两个波分量的数学公式也不同。群速度的公式为“v_g= dω/dk = v_p+ k dv_p / dk”，而相速度的公式为“v_p= ωk = λf”。

群速度和相速度之间的关系

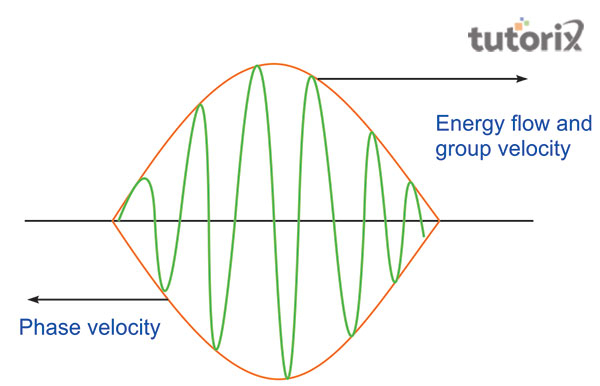
图 3：相速度和群速度之间的关系

“相速度”和“群速度”之间共享的关系指出，被认为是群速度的一组波的速度与这些波的“相速度”成“正比”。这种关系揭示了“相速度”和“群速度”之间的直接关系（Kondakci & Abouraddy，2019）。

基于这种关系，可以认为波的这两个分量相互依赖。

例如，可以说当波群的速度增加时，相速度的值将以相同的速率增加。另一方面，群速度的值将根据“相速度”的减小值而减小。

相速度和群速度之间的数学关系

“群速度”和“相速度”之间的数学关系如下：

为了获得波包的振幅，假设 ω 被认为是角速度，由“ω = 2πf”给出。K 代表角波数，由“k = 2π / λ”给出，字母 t 和 x 分别表示时间和位置。根据第一个方程“ω = kV_p”，k 的值为“dw / dk = V_p + k (dV_p/dk)”。基于此，获得的方程为“V_g = V_p + k (dV_p/dk)”，它显示了相速度和群速度之间的直接关系。

结论

本教程阐明了波的“群速度”的概念。此外，“相速度”被解释为波在任何介质中“传播”的速率。本教程包含了这两个“波的特性”之间的核心差异，并指出在“正常介质”中，“相速度”比“群速度”高。这两个特性之间形成的关系是这两个波的特性“彼此成正比”。

常见问题

Q1. 在“相速度”的上下文中，定义“色散”和“非色散正弦波”。

答：在色散波的情况下，指的是“相速度”，波的速度和速度在功能上是不同的，而在“非色散波”中，频率不同，但“不同波”的速度是统一的。

Q2. “相速度”和“波速”相同吗？

答：一般来说，如果概念中没有提出任何规范，波速通常称为相速度，因为它解释了相位在空间中传播时保持的特定速率。

Q3. 群速度在物理学中的作用是什么？

答：群速度的值有助于确定“波包传播”能量的速度。在“量子力学”中，运动粒子的位置的期望值由群速度理解。

Q4. 在什么情况下相速度和群速度相等？

答：在两个“单色波”穿过真空传播的情况下，这两个波的相速度变得相似，并且“叠加波”的相速度等同于“群速度”。