在一维数轴上表示线性不等式

---

介绍

线性方程是一种方程，其中方程中每个变量的阶数都恰好为 1。一元线性方程是一个只有一个变量并且对该方程只有一个解的方程。在图表上绘制时，它将显示为水平或垂直的直线。任何变量或符号都可以用来表示未知数，但变量“x”通常用于表示一元线性方程中的未知数。解决线性方程有几种简单的方法。将常数分离到方程的一侧，将变量分离到方程的另一侧，然后简化以获得最终答案。

一元线性方程是用来表示和解决未知量的基本方程。它很容易用图形表示，并且始终是一条直线。线性方程是表示数学语句的简单方法。在本教程中，我们将讨论在一维数轴上表示线性不等式。

线性不等式

将两个数学表达式等同起来的句子称为代数方程。线性方程（一阶方程）中变量的最大指数为 1。一元线性方程的标准形式为 $\mathrm{ax\:+\:b\:=\:0}$，其中 x 是变量。这意味着线性方程的变量没有像平方或立方这样的指数。它是一个方程或不等式，具有单个未知变量，并且产生直线模式而不是抛物线或任何其他非直线曲线。

这是一个线性方程 $\mathrm{y\:=\:2x\:+\:3}$ 的示例，在图上表示为一条直线。

这是另一个显示不等式图形的图形。此图的红线表示 $\mathrm{}x\:<\:5\:and\:x\:\geq\:-3$ 的图形。

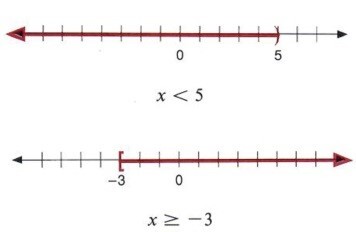
一元线性不等式

它类似于代数线性方程，但用不等号代替等号。当存在不等式时，LHS 和 RHS 之间存在不同的关系，例如大于或小于，而不是相等。例如 - 当 x <10 时，左右两侧之间存在不等式。这是一个 RHS 大于 LHS 的不等式示例。

符号“<”和“>”表示严格不等式，“≥”和“≤”表示松弛不等式。一元线性不等式的例子包括 𝑚𝑥 + 𝑛 > 0、𝑚𝑥 + 𝑛 < 0、𝑚𝑥 + 𝑛 ≤ 0 𝑎𝑛𝑑 𝑚𝑥 + 𝑛 ≥ 0。

注意 - 你迄今为止学到的关于解线性方程的所有知识也将用于解不等式。唯一的区别是，当你乘以或除以负数时，你还必须反转不等号。

数轴上线性不等式的表示

一元线性不等式：代数解法

我们知道不同类型的线性不等式。让我们检查一下这些不等式及其解。

以线性不等式为例。当 x 是整数时，3x <6。

不等式的 RHS 是 6，LHS 是 3x。当 x = 0 时，

$\mathrm{RHS\:=\:6\:,\:LHS\:=\:3\:\times\:0\:=\:0}$

由于 0 小于 6，因此 x = 0 满足不等式。当 x = 1 时，

$\mathrm{RHS\:=\:6\:,\:LHS\:=\:3}$.

由于 3 小于 6，因此 $\mathrm{x\:=\:1}$ 满足不等式。

$\mathrm{当\:x\:=\:2时}$,

$\mathrm{RHS\:=\:6\:,\:LHS\:=\:6}$

由于 6 不能小于 6，因此 x = 2 不满足不等式。已知为了满足不等式，x 必须小于 2。

“不等式的解”是使该陈述为真的变量的值。

因此，上述不等式的解为 0 和 1，称为解集。

线性不等式规则

规则 1 - 如果我们在每侧添加或减去相同的数字，不等式的符号不会改变。

规则 2 - 不等式可以在两侧除以或乘以相同的正值。如果两侧都乘以或除以负数，则不等号的符号将翻转。

绘制 $\mathrm{\lbrace\:a\:\rbrace\:x\:\leq\:0\:,\:\lbrace\:b\:\rbrace\:x\:>\:-2\:,\:\lbrace\:c\:\rbrace\:x\:<\:1\:,\:\lbrace\:d\:\rbrace\:x\:\geq\:-1}$ 的图形

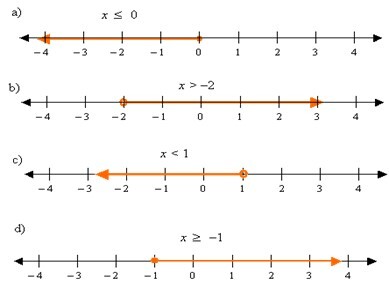
已解决的示例

示例 1 - 解 $\mathrm{2x\:+\:4\:\leq\:10}$，如果 x 为正，则在数轴上表示它。

解：给定方程为 $\mathrm{2x\:+\:4\:\leq\:10}$

现在分离变量和常数，即从两侧减去四，

$\mathrm{\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:2x\:+\:4\:-\:4\:\leq\:10\:-\:4}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:2x\:\leq\:6}$

两边除以 2，我们得到

$\mathrm{\Longrightarrow\:x\:\leq\:3}$

由于 x 为正（给定），因此 x 大于 0 且小于或等于 3，或

$\mathrm{x\:\varepsilon\:(0\:,\:3]}$

它可以表示为 -

示例 2 - 解 $\mathrm{2x\:+\:6\:<\:12}$ 并在图上表示

解 - 给定方程为 $\mathrm{2x\:+\:6\:<\:12}$

现在分离变量和常数，即从两侧减去六

$\mathrm{\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:2x\:+\:6\:-\:6\:<\:122\:-6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:2x\:<\:6}$

两边除以 2，我们得到

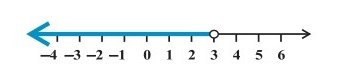
$\mathrm{\Longrightarrow\:x\:<\:3}$

此不等式可以表示为 -

结论

线性方程是直线方程，其中变量的幂为 1。它写成 𝑎𝑥 + 𝑏 = 0，其中 a 和 b 是整数，x 是变量。不等式是对两个表达式之间关系的断言。不等号 <、>、≤ 𝑜𝑟 ≥ 用于比较线性方程中两个表达式的值。一元线性方程和方程只有一个解或一个根。

常见问题解答

1. 一元线性方程是什么意思？

答：一元线性方程是直线方程，其中变量的幂为 1。它写成 $\mathrm{ax\:+\:b\:=\:0}$

2. 线性不等式是什么意思？

答：它类似于代数线性方程，但用不等号代替等号。

3. 不等号是什么？

不等号 <、>、≤ 𝑜𝑟 ≥ 用于比较线性方程中两个表达式的值。

4. 线性方程的次数是多少？

线性方程的次数为 1。

5. 线性不等式和等式的主要区别是什么？

唯一将不等式与线性方程区分开的是符号。在线性方程中，比较两个表达式，而在线性不等式中，将两个表达式等同。