标量和向量

---

简介

向量和标量都是物理量。前者既有方向又有大小，而后者只有大小，没有方向。物理量通常用作物理术语，如功、速度和力。它们被分为向量和标量两种量。

标量的定义

标量主要定义为一种物理量，它没有方向，只有大小。这种物理量通过其数值来定义，没有任何方向。这种量具有额外的性质，并且遵循简单的代数规则（Buttazzo等，2022）。

简单的代数规则主要是在这些量的幅值上进行加法运算。在物理学领域，使用了各种术语，例如速度、力、功和末速度。这些量根据其所属的领域进行划分，领域包括两种类型的量。

图 1：体积作为标量

这里可以给出标量的不同例子，包括温度、体积、时间、密度、速度、质量和距离。这些是这种类型的最常见例子（Danielson，2018）。

可以看出，这种量的幅值是用实数来描述的。这种量没有作用方向，这是它的一个特征。

矢量量的定义

矢量量是一种物理量，它既有大小又有方向。矢量量等于单位向量。此单位用小写字母û表示。这种类型的量既有大小又有方向（Bell等，2019）。可以看出，矢量的加法规则不遵循简单的代数规则。它用字母上的箭头或粗体字母表示。它用线段表示，并在末端有一个箭头。箭头主要描述线段的长度，给出大小。

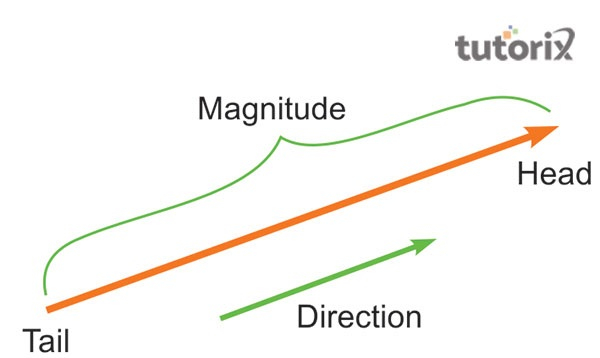
图 2：矢量量

矢量量包括速度、位移、动量、加速度、重量和力。这些是这种量的例子，并在当前时间具有应用。偏振和电场也是这种因素的两个常见例子。物理量与标量量是分开的。

标量和矢量的区别

矢量量是一个多维过程，而标量量是一个一维过程。这是这两个因素之间的一个重要区别。前者既有大小又有方向，而后者只有大小（Engineeringinsider.org，(2022)）。

标量在代数中具有普通作用，而矢量量具有独立的矢量代数。在方向和大小都发生变化时，矢量会发生变化，但标量仅在大小发生变化时才会发生变化。矢量不能分成两个矢量量，但标量可以分成另一个标量量。矢量包括速度和加速度，标量包括体积、质量、速度、电荷、电势和时间。

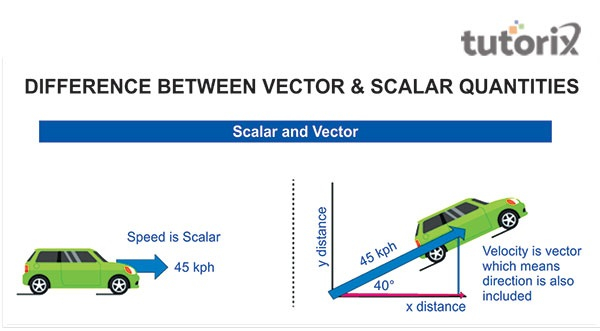
图 3：标量和矢量的区别

标量量没有方向，而矢量量有方向。物理量在其各自的领域具有不同的方面。这些是这两个因素之间的主要区别。

矢量的加法和减法

矢量量在加法和减法方面具有不同的方面。两种类型的定律有助于定义这种量的加法。第一种是三角形法则，另一种是平行四边形法则。第一种法则表示，当两个矢量用三角形的两条边表示时，三角形的第三条边（反向）表示三角形的合力（Askiitians.com，2022）。

另一方面，第二定律指出，当两个矢量在一点并排作用，并用平行四边形的两条边的方向和大小表示时，平行四边形的对角线表示它们的合力。减法的因素与加法过程相同。它是从另一个矢量中减去一个矢量的过程，它等效于矢量的加法。

矢量的特征

矢量量主要定义具有方向和大小特征的物理量。因此，这种量的主要特征是这个过程既有方向又有大小。这种类型的量不遵循代数规则（Grc.nasa.gov，2022）。矢量量的变化是方向或大小或两者兼而有之的变化。这些是这种量的特征，它不同于标量量。在前者的情况下，存在两个特征，而后者仅描述大小。

结论

矢量量和标量量是物理学中使用的物理量的类型。标量量只有大小，例如电荷和质量。另一方面，矢量量既有大小又有方向，例如重量和力。这些物理量在其领域也存在差异。

常见问题解答

Q1. 标量的例子是什么？

答：标量是一种只具有大小的物理量。这种量的一些例子是速度、质量、距离、体积、时间、温度和密度。

Q2. 矢量量的例子是什么？

答：矢量量既有方向又有大小。这种量的一些例子是偏振、力、动量、电场、角速度、加速度、线性动量、位移。

Q3. 矢量量加法过程的两个主要定律是什么？

答：三角形法则和平行四边形法则是描述矢量量加法过程的两种定律。这两种定律有助于矢量量的加法过程。