奇异值分解

机器学习使用奇异值分解的数学方法来理解庞大而复杂的数据集。

在这种数学方法中，一个唯一值矩阵 A 通过分解分解成三个矩阵。就 A 的组成部分而言，矩阵 A 的奇异值分解可以写成 A=UDVT。在这种情况下，S 表示 A 的奇异值，而 U 和 V 分别代表 A 的左奇异向量和右奇异向量。

数学算法

  • 给定矩阵 A，求矩阵 A 的转置 (AT)。

  • 求 A*AT

  • 求 A*AT 的特征向量

  • 使用公式 A*AT - λ I = 0 求特征向量，其中 I 是与 A 等价阶的单位矩阵。

  • 计算 A 的奇异值，方法是取 ATA 的特征值的平方根。奇异值按降序排列。

  • 我们计算 A 的左奇异向量和右奇异向量 −

    • 对于每个奇异值，找到 AT A 的相应特征向量。

    • 每个特征向量的长度都归一化为单位长度。

    • A 的左奇异向量是对应于 A 的非零奇异值的 A AT 的特征向量。

    • A 的右奇异向量是 AT A 的归一化特征向量。

  • A 的奇异值（按降序排列）由 S 的对角线元素表示。

    A 的左奇异向量由 U 的列表示

    V 的列表示 A 的右奇异向量。

示例 1

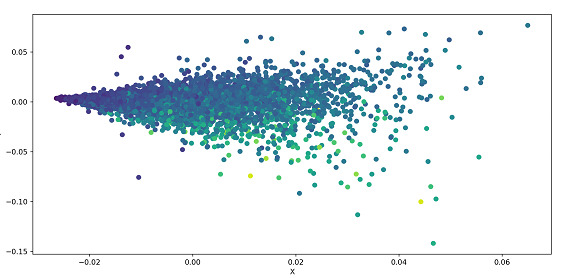
以下示例对数据集执行 SVD 并将其绘制为散点图。数据集从 UCI 数据集加载，数据根据参数进行分离。数据经过标准化处理，并将 .svd() 应用于数据（这是 Numpy 的 linalg（线性代数）模块的一部分）。使用散点图绘制数据。

算法

  • 步骤 1 − 导入 Pandas、Numpy 和 Matplotlib 库。

  • 步骤 2 − 将数据集的链接存储在 url 变量中。

  • 步骤 3 − 将特征（即数据集的列名）存储在名为 names 的数组中。

  • 步骤 4 − 使用 pd.read_csv() 方法读取数据

  • 步骤 5 − 特征与目标分离

  • 步骤 6 − 使用公式 (X - Xmean) / 标准差 X 标准化特征

  • 步骤 7 − 使用 Numpy 的 linalg 模块的 .svd() 方法对 X 执行 SVD

  • 步骤 8 − 构造对角矩阵 S

  • 步骤 9 − 使用 Matplotlib 的 .scatter() 方法绘制 U

  • 步骤 10 − 运行代码后，可以在弹出窗口中看到散点图

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


url='https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data'
names = ['Length', 'Diam', 'Height', 'Whole']
abalone = pd.read_csv(url, names=names)

X = abalone.iloc[:, :-1].values
y = abalone.iloc[:, -1].values

X = (X - X.mean(axis=0)) / X.std(axis=0)

U, s, Vt = np.linalg.svd(X, full_matrices=False)

S = np.diag(s)

plt.scatter(U[:, 0], U[:, 1], c=y)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

输出

示例 2

在以下示例中，我们计算矩阵 A 的 SVD，该矩阵作为参数传递给函数。我们计算特征向量和特征值，并按降序排列它们。该函数返回特征向量、奇异值和右奇异矩阵的转置。

算法

  • 步骤 1 − 导入 numpy 库

  • 步骤 2 − 定义一个函数 svd，它接受矩阵 A 作为输入

  • 步骤 3 − 使用 Numpy 的 linalg 方法的 .eigh() 方法计算 A^T * A 的特征值和特征向量。

  • 步骤 4 − 特征向量和特征值按降序排列。

  • 步骤 5 − 计算 A 的奇异值和右奇异向量

  • 步骤 6 − 该函数返回特征向量、奇异值和右奇异矩阵的转置。

  • 步骤 7 − 将值存储在数组 A 中，并使用 A 作为参数调用函数 svd

  • 步骤 8 − 将函数返回的值分别存储在 U、S、V 中并打印它们

import numpy as np
def svd(A):
   eigen_values, eigen_vectors = np.linalg.eigh(np.dot(A.T, A))
   
 
   sorted_indices = eigen_values.argsort()[::-1]
   eigen_values = eigen_values[sorted_indices]
   eigen_vectors = eigen_vectors[:,sorted_indices]
   
   singular_values = np.sqrt(eigen_values)
   right_singular_vectors = np.dot(A, eigen_vectors)
   right_singular_vectors /= singular_values
   
   return eigen_vectors, singular_values, right_singular_vectors.T
A = np.array([[1, 2, 2], [4, 5, 9], [7, 8, 10]])
U, S, V = svd(A)
print (U)
print (S)
print (V)

在上述代码中，svd() 函数以矩阵作为输入，并计算矩阵的特征值和特征向量。我们将计算出的特征值和特征向量按降序排列，并通过取特征值的平方根来计算奇异值并将它们存储在数组中。

然后，我们通过将矩阵与排序后的特征向量相乘并将结果除以之前计算的奇异值来计算右奇异向量。因此，该函数返回特征向量、奇异值和右奇异向量的转置。

输出

[[-0.43649583 -0.55427262 -0.70869828]
 [-0.52004753 -0.48734746  0.70145778]
 [-0.73418115  0.67474019 -0.07552297]]

[18.45494908  1.76319494  0.5531709 ]

[[-0.15957525 -0.59354546 -0.7888216 ]
 [-0.10179655  0.80469488 -0.58489624]
 [ 0.98192322 -0.01303565 -0.18883027]]

结论

奇异值分解有助于减少包含大量值的数据集。此外，此方法有助于为较小的值生成有意义的解决方案。但是，这些较小的值也包含原始数据中巨大的变异性。SVD 用于图像压缩中的低秩近似、推荐系统中的低秩近似、主成分分析和线性回归。

更新于：2023年8月7日

浏览量 329 次

开启您的 职业生涯

完成课程获得认证

开始学习
广告