照度平方反比定律（照明定律）

任何表面接收到的光线取决于该表面与光源的距离。平方反比定律给出了表面距离和表面照度之间的关系。

平方反比定律的陈述

平方反比定律指出：“表面的照度与该表面到点光源距离的平方成反比。”

解释

让我们考虑一个点光源'S'，其发光强度为'I'流明/球面度。如果两个面积分别为A₁和A₂的表面分别放置在距点光源'r'米和'R'米处。假设这些表面包含在相同的立体角'ω'内。

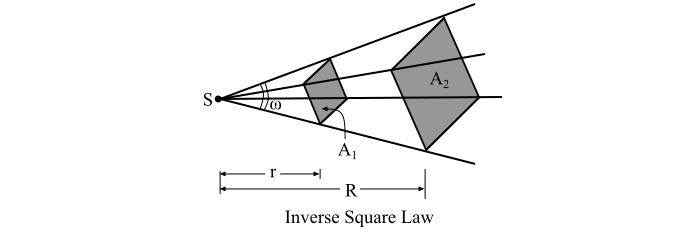
那么，表面接收到的总光通量由下式给出：

$$\mathrm{光通量,\phi \: =\:\mathit{I}\times \omega }$$

因此，面积A₁接收到的光通量为：

$$\mathrm{\phi_{1} \: =\:\mathit{I}\times \omega \: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

$$\mathrm{\because 立体角,\omega \: =\:\frac{面积}{距离^{2}} }$$

因此，面积A₁的立体角由下式给出：

$$\mathrm{\omega \: =\:\frac{\mathit{A}_{1}}{\mathit{r}^{2}}\: \: \cdot \cdot \cdot \left ( 2 \right ) }$$

因此，表面积A₁上的总光通量为：

$$\mathrm{\phi _{1}\: =\:\frac{\mathit{I\times A_{\mathrm{1}}}}{\mathit{r^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 3 \right )}$$

$$\mathrm{\because 照度,\mathit{E}\: =\:\frac{光通量\left ( \phi \right )}{面积\, \left ( \mathit{A} \right )} }$$

因此，表面A₁的照度为

$$\mathrm{\mathit{E} _{1}\: =\:\frac{\phi _{1}}{\mathit{A}_{1}}\: =\:\frac{\mathit{I\times A_{\mathrm{1}}}}{\mathit{r^{\mathrm{2}}}}\times \frac{1}{\mathit{A}_{1}}\: =\:\mathit{\frac{I}{r^{\mathrm{2}}}}\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$

类似地，放置在距光源'R'米处并包含在相同立体角'ω'内的表面A2上的总光通量由下式给出：

$$\mathrm{\phi _{2}\: =\:\mathit{I}\times \omega \: =\:\mathit{I\times \frac{A_{\mathrm{2}}}{\left ( R \right )^{\mathrm{2}}}} }$$

$$\mathrm{\therefore \phi _{2}\: =\:\mathit{ \frac{I\times A_{\mathrm{2}}}{R^{\mathrm{2}}}}}$$

因此，表面A2的照度由下式给出：

$$\mathrm{\mathit{E} _{2}\: =\:\frac{\phi _{2}}{\mathit{A}_{2}}\: =\:\frac{\mathit{I\times A_{\mathrm{2}}}}{\mathit{R^{\mathrm{2}}}}\times \frac{1}{\mathit{A}_{2}}}$$

$$\mathrm{\therefore \mathit{E} _{2}\: =\:\frac{\mathit{I}}{\mathit{R}^{\mathrm{2}}}\: \cdot \cdot \cdot \left ( 5 \right )}$$

因此，从公式(4)和(5)，我们有：

$$\mathrm{\mathit{E}_{1}:\mathit{E}_{2}::\frac{\mathit{I}}{\mathit{r}^{2}}:\frac{\mathit{I}}{\mathit{R}^{2}}}$$

此表达式称为**照度平方反比定律**。从该表达式可以看出，照度与光源和表面之间距离的平方成反比。此关系可应用于所有光源。

Saini Manish Kumar

更新于：2022年4月5日

7000+ 浏览量

开启您的职业生涯

完成课程获得认证

开始学习