什么是朗伯余弦定律？（照明定律）

任何表面接收到的光线取决于该表面的法线与光通量之间的夹角。朗伯余弦定律解释了表面照度与角度余弦之间的关系。

说明

朗伯余弦照明定律指出：

“表面的照度与其法线与入射光方向之间夹角的余弦成正比”。

也就是说，

$$\mathrm{\mathit{E}\propto cos\, \theta \: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

解释

情况一 – 考虑一个垂直于光通量的表面，如图1所示。

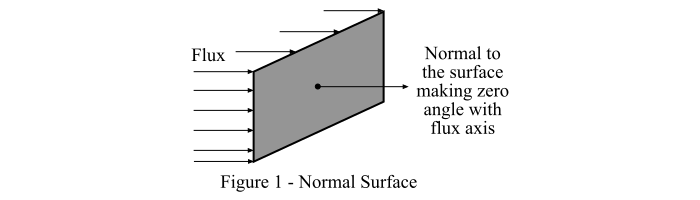
然后，根据朗伯余弦定律，我们得到：

$$\mathrm{照度,\mathit{E}=\frac{\phi }{\mathit{A}}\: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$

情况二 – 考虑一个相对于光通量倾斜的表面，该表面的法线与光通量轴线成一个角度 (θ)，如图2所示。

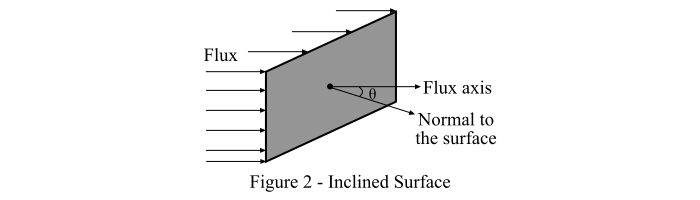
然后，根据朗伯余弦定律，我们得到：

$$\mathrm{\mathit{E}=\frac{\phi }{\mathit{A}}\times cos\, \theta \: \: \: \cdot \cdot \cdot \left ( 3 \right )}$$

情况三 – 考虑平面表面上的一个点 'P'，光源 (S) 与点 'P' 之间的距离为 'r' 米。光源 (S) 位于距表面 'h' 米的高度，其发光强度为 'I' 坎德拉，如图3所示。

然后，根据余弦照明定律，我们得到点 'P' 的照度为：

$$\mathrm{\mathit{E_{P}}=\mathit{\frac{I }{r^{\mathrm{2}}}}\times cos\, \theta}$$

从图3，我们有：

$$\mathrm{cos\, \theta \: =\: \mathit{\frac{h}{r}}}$$

$$\mathrm{\Rightarrow \mathit{r} \: =\: \frac{\mathit{h}}{cos\, \theta}}$$

因此，点 'P' 的照度为：

$$\mathrm{\mathit{E_{P}}\: =\: \mathit{\frac{I }{\left ( \mathit{h}/\mathrm{cos\, \theta }\right )^{\mathrm{2}}}}\times cos\, \theta}$$

$$\mathrm{\therefore \mathit{E_{P}}\: =\: \mathit{\frac{I }{\mathit{h}^{\mathrm{2}}}}\times cos^{3}\, \theta\: \: \: \cdot \cdot \cdot \left ( 4 \right )}$$

其中，I/h² 是位于光源正下方的任何点的照度。

Saini Manish Kumar

更新于：2022年4月6日

11K+ 次浏览

开启你的职业生涯

完成课程获得认证

开始学习