数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究法拉第定律和楞次定律
法拉第电磁感应定律
迈克尔·法拉第（一位英国科学家）进行了一系列实验来演示电磁感应现象，并将他的结论总结成两个定律，称为法拉第电磁感应定律。
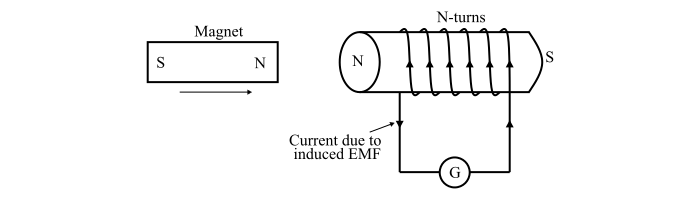
电磁感应第一定律
第一定律指出“当穿过导体或线圈的磁通量发生变化时，导体或线圈中就会感应出电动势”。因此，第一定律说明了在什么条件下导体或线圈中会感应出电动势。
电磁感应第二定律
第二定律指出“导体或线圈中感应电动势的大小与磁通量变化率成正比”。因此，第二定律给出了导体或线圈中感应电动势的大小。
解释 - 考虑一个具有 N 个匝数的线圈，并且穿过该线圈的磁通量在 t 秒内从 $\varphi_{1}$ 变为 $\varphi_{2}$。因此，
$$\mathrm{初始磁通链数,ψ_{1} = N\varphi_{1}}$$
$$\mathrm{最终磁通链数, ψ_{2} = N\varphi_{2}}$$
$$\mathrm{\therefore 感应电动势,e\propto\frac{ψ_2-ψ_1}{t}\propto\frac{N\varphi_2-N\varphi_1}{t}}$$
$$\mathrm{\Longrightarrow e=k(\frac{N\varphi_2-N\varphi_1}{t})}$$
其中 k 是比例常数，在 SI 单位中其值为 1。因此，
$$\mathrm{\Longrightarrow e=(\frac{N\varphi_2-N\varphi_1}{t})}$$
微分形式为：
$$\mathrm{e=N\frac{d\varphi}{dt}}$$
上述公式从数学上表示了法拉第第二定律。
楞次定律
一位德国科学家，埃米尔·楞次，给出了一个确定导体或线圈中电磁感应感应电动势方向的规则，其陈述如下：
“感应电动势产生的电流的方向将与产生它的原因相反，即感应电动势产生的电流将建立一个磁通量来抵消产生它的磁通量变化”。
数学上，楞次定律通过在法拉第第二定律的右侧添加一个负号来表示，即
$$\mathrm{e=-N\frac{d\varphi}{dt}}$$
这里，负号表示感应电动势与感应它的变化磁场相反。因此，楞次定律直接遵循能量守恒定律，即为了在线圈或导体中感应出电动势，必须在阻力中消耗一些能量。
数值示例
一个 600 匝线圈与 25 mWb 的磁通量相关联。如果此磁通量在 3 毫秒内反向，则计算线圈中感应的电动势。
解答
$$\mathrm{磁通量变化,d\varphi=\varphi_{2} - \varphi_{1}=25-(-25)=50nmb}$$
$$\mathrm{变化所需时间,dt=3ms}$$
$$\mathrm{\therefore 感应电动势,e = N\frac{d\varphi}{dt}=600\times(\frac{50\times10^{-3}{3}}\times10^{-3})=10000=10kV}$$
543 次浏览
